题目内容
(08年浙江卷理)(本题14分)
已知数列![]() ,
,![]() ,
,![]() ,
,![]() .记:
.记:
![]() .
.![]() .
.
求证:当![]() 时,
时,
(Ⅰ)![]() ;
;
(Ⅱ)![]() ;
;
(Ⅲ)![]() .
.
本题主要考查数列的递推关系,数学归纳法、不等式证明等基础知识和基本技能,
同时考查逻辑推理能力.满分14分.
(Ⅰ)证明:用数学归纳法证明.
① 当![]() 时,因为
时,因为![]() 是方程
是方程![]() 的正根,所以
的正根,所以![]() .
.
② 假设当![]() 时,
时,![]() ,
,
因为![]()
![]()
![]() ,
,
所以![]() .
.
即当![]() 时,
时,![]() 也成立.
也成立.
根据①和②,可知![]() 对任何
对任何![]() 都成立.
都成立.
(Ⅱ)证明:由![]() ,
,![]() (
(![]() ),
),
得![]() .
.
因为![]() ,所以
,所以![]() .
.
由![]() 及
及![]() 得
得![]() ,
,
所以![]() .
.
(Ⅲ)证明:由![]() ,得
,得
![]() ,
,
所以 ![]() ,
,
于是 ![]() ,
,
故当![]() 时,
时,![]() ,
,
又因为![]() ,
,
所以![]() .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
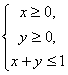 时,恒有
时,恒有