题目内容
在三种产品,合格率分别是0.90,0.95和0.95,各抽取一件进行检验.(Ⅰ)求恰有一件不合格的概率;
(Ⅱ)求至少有两件不合格的概率.(精确到0.001)
【答案】分析:(1)要求恰有一件不合格的概率,我们根据P=P(A•B•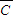 )+P(A•
)+P(A•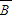 •C)+P(
•C)+P( •B•C),根据已知条件,算出式中各数据量的值,代入公式即可求解.
•B•C),根据已知条件,算出式中各数据量的值,代入公式即可求解.
(2)我们可以根据至少有两件不合格的概率公式P=P(A•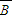 •
•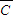 )+P(
)+P(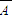 •B•
•B•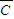 )+P(
)+P( •
• •C)+P(
•C)+P( •
•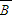 •
• ),根据已知条件,算出式中各数据量的值,代入公式即可求解.也可以从对立事件出发根据(1)的结论,利用P=1-P(A•B•C)+P(A•B•
),根据已知条件,算出式中各数据量的值,代入公式即可求解.也可以从对立事件出发根据(1)的结论,利用P=1-P(A•B•C)+P(A•B•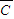 )+P(A•
)+P(A•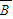 •C)+P(
•C)+P(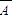 •B•C)进行求解.
•B•C)进行求解.
解答:解:设三种产品各抽取一件,
抽到合格产品的事件分别为A、B和C.
(Ⅰ)P(A)=0.90,P(B)=P(C)=0.95.
P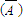 =0.10,P
=0.10,P =P
=P =0.05.
=0.05.
因为事件A,B,C相互独立,
恰有一件不合格的概率为
P(A•B• )+P(A•
)+P(A• •C)+P(
•C)+P( •B•C)
•B•C)
=P(A)•P(B)•P(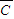 )+P(A)•P(
)+P(A)•P(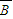 )•P(C)+P(
)•P(C)+P( )•P(B)•P(C)
)•P(B)•P(C)
=2×0.90×0.95×0.05+0.10×0.95×0.95=0.176
答:恰有一件不合格的概率为0.176;
(Ⅱ)解法一:至少有两件不合格的概率为
P(A• •
•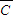 )+P(
)+P( •B•
•B•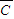 )+P(
)+P(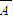 •
•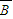 •C)+P(
•C)+P( •
•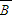 •
•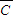 )
)
=0.90×0.052+2×0.10×0.05×0.95+0.10×0.052
=0.012.
答:至少有两件不合格的概率为0.012.
解法二:三件产品都合格的概率为
P(A•B•C)=P(A)•P(B)•P(C)
=0.90×0.952
=0.812.
由(Ⅰ)知,恰有一件不合格的概率为0.176,
所以至少有两件不合格的概率为
1-P(A•B•C)+0.176
=1-(0.812+0.176)
=0.012.
答:至少有两件不合格的概率为0.012.
点评:本小题主要考查相互独立事件概率的计算,运用数学知识解决问题的能力,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.
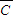 )+P(A•
)+P(A•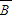 •C)+P(
•C)+P( •B•C),根据已知条件,算出式中各数据量的值,代入公式即可求解.
•B•C),根据已知条件,算出式中各数据量的值,代入公式即可求解.(2)我们可以根据至少有两件不合格的概率公式P=P(A•
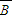 •
•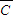 )+P(
)+P(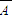 •B•
•B•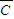 )+P(
)+P( •
• •C)+P(
•C)+P( •
•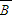 •
• ),根据已知条件,算出式中各数据量的值,代入公式即可求解.也可以从对立事件出发根据(1)的结论,利用P=1-P(A•B•C)+P(A•B•
),根据已知条件,算出式中各数据量的值,代入公式即可求解.也可以从对立事件出发根据(1)的结论,利用P=1-P(A•B•C)+P(A•B•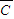 )+P(A•
)+P(A•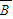 •C)+P(
•C)+P(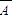 •B•C)进行求解.
•B•C)进行求解.解答:解:设三种产品各抽取一件,
抽到合格产品的事件分别为A、B和C.
(Ⅰ)P(A)=0.90,P(B)=P(C)=0.95.
P
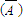 =0.10,P
=0.10,P =P
=P =0.05.
=0.05.因为事件A,B,C相互独立,
恰有一件不合格的概率为
P(A•B•
 )+P(A•
)+P(A• •C)+P(
•C)+P( •B•C)
•B•C)=P(A)•P(B)•P(
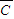 )+P(A)•P(
)+P(A)•P(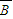 )•P(C)+P(
)•P(C)+P( )•P(B)•P(C)
)•P(B)•P(C)=2×0.90×0.95×0.05+0.10×0.95×0.95=0.176
答:恰有一件不合格的概率为0.176;
(Ⅱ)解法一:至少有两件不合格的概率为
P(A•
 •
•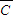 )+P(
)+P( •B•
•B•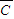 )+P(
)+P(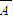 •
•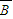 •C)+P(
•C)+P( •
•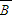 •
•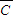 )
)=0.90×0.052+2×0.10×0.05×0.95+0.10×0.052
=0.012.
答:至少有两件不合格的概率为0.012.
解法二:三件产品都合格的概率为
P(A•B•C)=P(A)•P(B)•P(C)
=0.90×0.952
=0.812.
由(Ⅰ)知,恰有一件不合格的概率为0.176,
所以至少有两件不合格的概率为
1-P(A•B•C)+0.176
=1-(0.812+0.176)
=0.012.
答:至少有两件不合格的概率为0.012.
点评:本小题主要考查相互独立事件概率的计算,运用数学知识解决问题的能力,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.

练习册系列答案
相关题目