题目内容
数列 的前n项和
的前n项和 =
=
 的前n项和
的前n项和 =
= 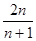
本试题主要是考查了数列的求和的运用。
因为数列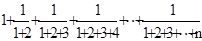 可知第n项可知变形为
可知第n项可知变形为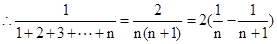 ,因此可知前n项和利用裂项求和的思想可知为
,因此可知前n项和利用裂项求和的思想可知为 =2(1-
=2(1-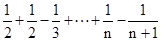 )=
)=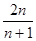 ,故答案为
,故答案为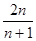 。
。
解决该试题的关键是利用 ,采用裂项法得到和式。
,采用裂项法得到和式。
因为数列
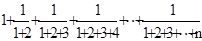 可知第n项可知变形为
可知第n项可知变形为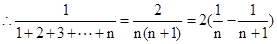 ,因此可知前n项和利用裂项求和的思想可知为
,因此可知前n项和利用裂项求和的思想可知为 =2(1-
=2(1-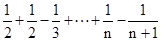 )=
)=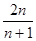 ,故答案为
,故答案为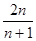 。
。解决该试题的关键是利用
 ,采用裂项法得到和式。
,采用裂项法得到和式。
练习册系列答案
相关题目
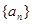 的通项公式
的通项公式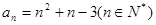 ,则
,则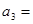 .
. 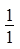 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 ……依次排列到第
……依次排列到第 项属于的范围是( )。
项属于的范围是( )。



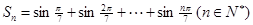 ,则在
,则在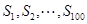 中,正数的个数是
中,正数的个数是 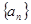 中, 已知
中, 已知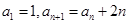 , 则
, 则 ________________;
________________;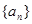 满足递推式
满足递推式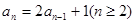 ,其中
,其中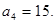
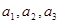 ;
;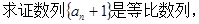 并求数列
并求数列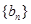 有
有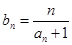 求数列
求数列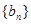 的前n项和
的前n项和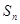 .
.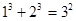 ,
,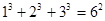 ,
,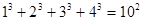 根据上述规律,
根据上述规律,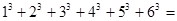 ( )
( )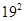



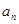 }中,
}中,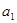 =
=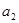 =1,
=1, 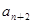 =
=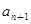 +
+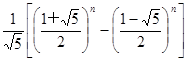 ,根据上述结论,可以知道不超过实数
,根据上述结论,可以知道不超过实数 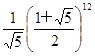 的最大整数为
的最大整数为 

