题目内容
下列函数中,满足“对任意x1,x2∈(0,+∞),都有 >0成立”的是
>0成立”的是
- A.f(x)=

- B.f(x)=ln(x+1)
- C.f(x)=

- D.f(x)=|x-1|
B
分析:由题意知f(x)在(0,+∞)上单调递增,据此对选项逐项判断即可.
解答:由题意:对任意x1,x2∈(0,+∞),都有 >0成立,知f(x)在(0,+∞)上单调递增,
>0成立,知f(x)在(0,+∞)上单调递增,
f(x)= 在(0,+∞)上递减,故排除A;
在(0,+∞)上递减,故排除A;
f(x)= 在(0,+∞)上递减,故排除C;
在(0,+∞)上递减,故排除C;
f(x)=|x-1|在(-∞,1]上递减,在[1,+∞)上递增,所以f(x)在(0,+∞)上不单调,故排除D;
而f(x)=ln(1+x)在(0,+∞)上递增,
故选B.
点评:本题考查基本函数的单调性,熟练掌握基本函数的单调性是解决本题的基础,解决本题的关键是正确理解题意,对问题进行合理转化.
分析:由题意知f(x)在(0,+∞)上单调递增,据此对选项逐项判断即可.
解答:由题意:对任意x1,x2∈(0,+∞),都有
 >0成立,知f(x)在(0,+∞)上单调递增,
>0成立,知f(x)在(0,+∞)上单调递增,f(x)=
 在(0,+∞)上递减,故排除A;
在(0,+∞)上递减,故排除A;f(x)=
 在(0,+∞)上递减,故排除C;
在(0,+∞)上递减,故排除C;f(x)=|x-1|在(-∞,1]上递减,在[1,+∞)上递增,所以f(x)在(0,+∞)上不单调,故排除D;
而f(x)=ln(1+x)在(0,+∞)上递增,
故选B.
点评:本题考查基本函数的单调性,熟练掌握基本函数的单调性是解决本题的基础,解决本题的关键是正确理解题意,对问题进行合理转化.

练习册系列答案
相关题目
 中,满足“对任意
中,满足“对任意 ,
,
 (0,
(0, ),当
),当 >
> 的是(
)
的是(
)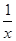 B.
B.
 C .
C . D.
D.