题目内容
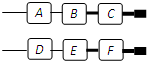
将图中编有号的五个区域染色，有五种颜色可供选择，要求有公共边的两个区域不能同色，则不同的涂色方法总数为______（用数字作答）．
先涂1区，再涂2、4区，最后涂3、5区．
若2、4区同色，则3、5区各有3种方法，故共有5×4×3×3=180种不同的方法．
若2、4区不同色，则3、5区各有2种方法，故共有5×4×3×2×2=240种不同的方法．
根据分类计数原理，所有的不同方法共有180+240=420种，
故答案为：420．
若2、4区同色，则3、5区各有3种方法，故共有5×4×3×3=180种不同的方法．
若2、4区不同色，则3、5区各有2种方法，故共有5×4×3×2×2=240种不同的方法．
根据分类计数原理，所有的不同方法共有180+240=420种，
故答案为：420．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
