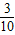Question

从长度分别为1cm、3cm、5cm、7cm、9cm的5条线段中任取3条作为三角形的三边，能构成三角形的概率为（　　）

• A、

  3

  10

• B、

  3

  5

• C、

  2

  5

• D、

  1

  5

Answer 1

分析：列举出所有情况，让这3条线段能构成三角形的情况数除以总情况数即为所求的概率．

解答：解：任取其中的3条，共有C₅³=10种结果，并且每个结果出现的机会相同，
能构成三角形的有（3，5，7）；（3，5，9）；（5，7，9）共有3种情况，
∴P（这3条线段能构成三角形）=

3

10

．
故选A．

点评：本题是一个列举法求概率与三角形的三边关系相结合的题目．用到的知识点为：概率=所求情况数与总情况数之比．构成三角形的基本要求为两小边之和大于最大边．