题目内容
 已知如图是函数y=2sin(ωx+φ)(|φ|<
已知如图是函数y=2sin(ωx+φ)(|φ|<| π |
| 2 |
分析:根据周期可求得ω值,利用五点法作图的过程得2×
+φ=
,由此可求φ值.
| π |
| 6 |
| π |
| 2 |
解答:解:由图象知函数周期T=
π-(-
)=π,
所以ω=
=2.
又函数图象过点(
,2),由五点法作图得,2×
+φ=
,解得φ=
.
所以ω=2,φ=
.
故选C.
| 11 |
| 12 |
| π |
| 12 |
所以ω=
| 2π |
| π |
又函数图象过点(
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
所以ω=2,φ=
| π |
| 6 |
故选C.
点评:本题考查五点作图的方法,在一个周期内,图象上的五个关键点的横坐标分别为:0,
,π,
,2π.
| π |
| 2 |
| 3π |
| 2 |

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
已知如图是函数y=2sin(ωx+φ)(|φ|<
)的图象,那么( )
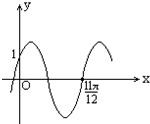
| π |
| 2 |

A、?=
| ||||
B、?=
| ||||
C、?=2,φ=
| ||||
D、?=2,φ=-
|
 )图像上的一段,则( )
)图像上的一段,则( ) ,φ=
,φ= (B)ω=
(B)ω=
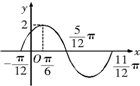
 )的图象上的一段,则( )
)的图象上的一段,则( )
 ,φ=
,φ=
 ,φ=-
,φ=-

