题目内容
已知函数 ,若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
,若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )A.(0,1)
B.(0,2)
C.(1,2)
D.(0,3)
【答案】分析:由已知中函数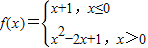 ,若关于x的方程f2(x)-af(x)=0恰有五个不同的实数解,我们可以根据函数f(x)的图象分析出实数a的取值范围.
,若关于x的方程f2(x)-af(x)=0恰有五个不同的实数解,我们可以根据函数f(x)的图象分析出实数a的取值范围.
解答:解:函数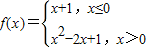 的图象如下图所示:
的图象如下图所示:
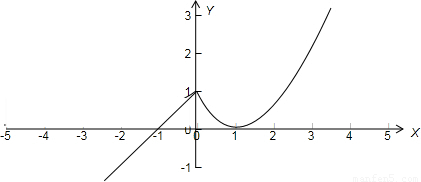
关于x的方程f2(x)=af(x)可转化为:
f(x)=0,或f(x)=a,
若关于x的方程f2(x)=af(x)恰有五个不同的实数解,
则f(x)=a恰有三个不同的实数解,
由图可知:0<a<1
故选A
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据已知中函数的解析式,画出函数的图象,再利用数形结合是解答本题的关键.
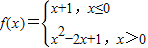 ,若关于x的方程f2(x)-af(x)=0恰有五个不同的实数解,我们可以根据函数f(x)的图象分析出实数a的取值范围.
,若关于x的方程f2(x)-af(x)=0恰有五个不同的实数解,我们可以根据函数f(x)的图象分析出实数a的取值范围.解答:解:函数
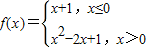 的图象如下图所示:
的图象如下图所示:
关于x的方程f2(x)=af(x)可转化为:
f(x)=0,或f(x)=a,
若关于x的方程f2(x)=af(x)恰有五个不同的实数解,
则f(x)=a恰有三个不同的实数解,
由图可知:0<a<1
故选A
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据已知中函数的解析式,画出函数的图象,再利用数形结合是解答本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 ,若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )
,若关于x的方程f2(x)-af(x)=0恰有5个不同的实数解,则a的取值范围是( )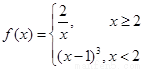 ,若关于x的方程
,若关于x的方程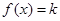 有两个不同的实根,则实数k的取值范围是
.
有两个不同的实根,则实数k的取值范围是
.  若关于x的方程
若关于x的方程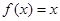 有且仅有二个不等实根,则实数a的取值范围是( )
有且仅有二个不等实根,则实数a的取值范围是( ) B.(
B.( ) C.
) C. D.(-3,-2]
D.(-3,-2]