题目内容
存在x<0使得不等式x2<2-|x-t|成立,则实数t的取值范围是
(-
,2)
| 9 |
| 4 |
(-
,2)
.| 9 |
| 4 |
分析:本题利用纯代数讨论是很繁琐的,要用数形结合.原不等式x2<2-|x-t|,即|x-t|<2-x2,分别画出函数y1=|x-t|,y2=2-x2,这个很明确,是一个开口向下,关于y轴对称,最大值为2的抛物线;要存在x<0使不等式|x-t|<2-x2成立,则y1的图象应该在第二象限(x<0)和y2的图象有交点,再分两种临界讲座情况,当t≤0时,y1的右半部分和y2在第二象限相切;当t>0时,要使y1和y2在第二象限有交点,最后综上得出实数t的取值范围.
解答:
 解:不等式x2<2-|x-t|,即|x-t|<2-x2,
解:不等式x2<2-|x-t|,即|x-t|<2-x2,
令y1=|x-t|,y1的图象是关于x=t对称的一个V字形图形,其象位于第一、二象限;
y2=2-x2,是一个开口向下,关于y轴对称,最大值为2的抛物线;
要存在x<0,使不等式|x-t|<2-x2成立,则y1的图象应该在第二象限和y2的图象有交点,两种临界情况,①当t≤0时,y1的右半部分和y2在第二象限相切:
y1的右半部分即y1=x-t,
联列方程y=x-t,y=2-x2,只有一个解;
即x-t=2-x2,即x2+x-t-2=0,△=1+4t+8=0,得:t=-
;
此时y1恒大于等于y2,所以t=-
取不到;
所以-
<t≤0;
②当t>0时,要使y1和y2在第二象限有交点,
即y1的左半部分和y2的交点的位于第二象限;
无需联列方程,只要y1与y轴的交点小于2即可;
y1=t-x与y轴的交点为(0,t),所以t<2,
又因为t>0,所以0<t<2;
综上,实数t的取值范围是:-
<t<2;
故答案为:(-
,2).

 解:不等式x2<2-|x-t|,即|x-t|<2-x2,
解:不等式x2<2-|x-t|,即|x-t|<2-x2,令y1=|x-t|,y1的图象是关于x=t对称的一个V字形图形,其象位于第一、二象限;
y2=2-x2,是一个开口向下,关于y轴对称,最大值为2的抛物线;
要存在x<0,使不等式|x-t|<2-x2成立,则y1的图象应该在第二象限和y2的图象有交点,两种临界情况,①当t≤0时,y1的右半部分和y2在第二象限相切:
y1的右半部分即y1=x-t,
联列方程y=x-t,y=2-x2,只有一个解;
即x-t=2-x2,即x2+x-t-2=0,△=1+4t+8=0,得:t=-
| 9 |
| 4 |
此时y1恒大于等于y2,所以t=-
| 9 |
| 4 |
所以-
| 9 |
| 4 |
②当t>0时,要使y1和y2在第二象限有交点,
即y1的左半部分和y2的交点的位于第二象限;
无需联列方程,只要y1与y轴的交点小于2即可;
y1=t-x与y轴的交点为(0,t),所以t<2,
又因为t>0,所以0<t<2;
综上,实数t的取值范围是:-
| 9 |
| 4 |
故答案为:(-
| 9 |
| 4 |
点评:本小题主要考查函数图象的应用、二次函数、绝对值不等式等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
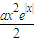 对于n∈R恒成立.
对于n∈R恒成立.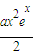 成立?如果存在,求出符合条件的一个x;否则说明理由.
成立?如果存在,求出符合条件的一个x;否则说明理由.