Question

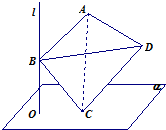
如图，直线l⊥平面α，垂足为O，正四面体ABCD的棱长为4，C在平面α内，B是直线l上的动点，则当O到AD的距离为最大时，正四面体在平面α上的射影面积为（　　）

A．4+2 2

B．2 2 +2

C．4

D．4 3

Answer 1

由题意，直线BC与动点O的空间关系：点O是以BC为直径的球面上的点，所以O到AD的距离为四面体上以BC为直径的球面上的点到AD的距离，最大距离为AD到球心的距离（即BC与AD的公垂线）+半径=2

2

+2．
再考虑取得最大距离时四面体的投影情况，此时我们注意到AD垂直平面OBC，且平行平面α，故其投影是以AD为底，O到AD 的距离投影，即（2

2

+2）cos45°=2+

2

为高的等腰三角形，其面积=

1

2

×4×（2+

2

）=4+2

2

．
故选A．