题目内容
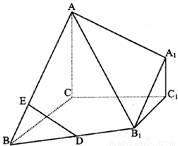
 如图,在三棱台ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=∠BC1C=90°,A1C1=a,C1B=2a.
如图,在三棱台ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=∠BC1C=90°,A1C1=a,C1B=2a.(I)求证AB⊥平面AA1C1C;
(II)求证C1C⊥平面ABC1;
(III)求AC与BC1所成的角.
分析:(I)证明AB垂直平面AA1C1C内的两条相交直线AA1,AC,即可证明结论;
(II)只需证明C1C垂直平面ABC1内的两条相交直线AB,BC1,即可证明直线与平面垂直;
(III)连接A1B,说明AC与BC1所成的角是∠BC1A1(或它的补角)通过证明三角形A1C1B是直角三角形,即可求解AC与BC1所成的角.
(II)只需证明C1C垂直平面ABC1内的两条相交直线AB,BC1,即可证明直线与平面垂直;
(III)连接A1B,说明AC与BC1所成的角是∠BC1A1(或它的补角)通过证明三角形A1C1B是直角三角形,即可求解AC与BC1所成的角.
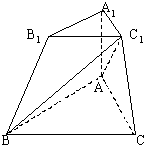
解答: 解:(I)∵侧棱AA1⊥平面ABC,
解:(I)∵侧棱AA1⊥平面ABC,
AB?平面ABC,∴AA1⊥AB,
又∵∠BAC=90°∴AB⊥AC,
AA1∩AC=A,
从而AB⊥平面AA1C1C…(4分)
(II)由(I)可知AB⊥平面AA1C1C,C1C?平面AA1C1C,
∴C1C⊥AB
又∵C1C⊥BC1并且AB∩BC1=B,
∴C1C⊥平面ABC1…(8分)
(III)连接A1B,∵AC∥A1C1∴AC与BC1所成的角是∠BC1A1(或它的补角)
∵A1C1⊥A1B1,A1C1⊥A1A,,A1A∩A1B1=A1,∴A1C1⊥平面A1ABB1
∵BA1?平面A1ABB1∴A1C1⊥A1B
在直角三角形A1C1B中,A1C1=a,C1B=2a
∠BC1A1=60°
即 异面直线AC与BC1所成的角为60°…(15分)
 解:(I)∵侧棱AA1⊥平面ABC,
解:(I)∵侧棱AA1⊥平面ABC,AB?平面ABC,∴AA1⊥AB,
又∵∠BAC=90°∴AB⊥AC,
AA1∩AC=A,
从而AB⊥平面AA1C1C…(4分)
(II)由(I)可知AB⊥平面AA1C1C,C1C?平面AA1C1C,
∴C1C⊥AB
又∵C1C⊥BC1并且AB∩BC1=B,
∴C1C⊥平面ABC1…(8分)
(III)连接A1B,∵AC∥A1C1∴AC与BC1所成的角是∠BC1A1(或它的补角)
∵A1C1⊥A1B1,A1C1⊥A1A,,A1A∩A1B1=A1,∴A1C1⊥平面A1ABB1
∵BA1?平面A1ABB1∴A1C1⊥A1B
在直角三角形A1C1B中,A1C1=a,C1B=2a
∠BC1A1=60°
即 异面直线AC与BC1所成的角为60°…(15分)
点评:本题是中档题,考查直线与平面垂直的证明,直线与直线所成的角的判断与求解,考查空间想象能力,计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
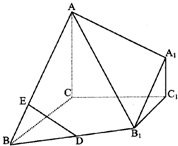 如图,在三棱台ABC-A1B1C1中,CA,CB,CC1两两垂直且长度相等,B1C1=
如图,在三棱台ABC-A1B1C1中,CA,CB,CC1两两垂直且长度相等,B1C1= 如图,在三棱台ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=∠BC1C=90°,A1C1=a,C1B=2a.
如图,在三棱台ABC-A1B1C1中,侧棱AA1⊥底面ABC,∠BAC=∠BC1C=90°,A1C1=a,C1B=2a.
 BC,D为BB1中点,E为AB上一点,且BE=
BC,D为BB1中点,E为AB上一点,且BE= BA,
BA,