题目内容
已知平面α、β和不在这两个平面内的两直线m、n,下列命题中
命题1:若α⊥β,m⊥n,m∥α,则n∥β
命题2:若α⊥β,m∥n,m∥α,则n⊥β
命题3:若α∥β,m∥n,m⊥α,则n⊥β
命题4:若α∥β,m⊥n,m⊥α,则n∥β
真命题的个数是
- A.4个
- B.3个
- C.2个
- D.个
C
分析:平面α、β和不在这两个平面内的两直线m、n:若α⊥β,m⊥n,m∥α,则n∥β或n与β相交;若α⊥β,m∥n,m∥α,则n∥β或n与β相交;若α∥β,m⊥α,则m⊥β,若m∥n,则n⊥β;若α∥β,m⊥α,则m⊥β,若m⊥n,则n∥β.
解答:平面α、β和不在这两个平面内的两直线m、n,
命题1:若α⊥β,m⊥n,m∥α,则n∥β或n与β相交,故命题1不正确;
命题2:若α⊥β,m∥n,m∥α,则n∥β或n与β相交,命题2不正确;
命题3:若α∥β,m⊥α,则m⊥β;若m∥n,则n⊥β,故命题3正确;
命题4:若α∥β,m⊥α,则m⊥β;若m⊥n,则n∥β,故命题4正确.
故选C.
点评:本题考查平面的基本性质及推论,是基础题.解题时要认真审题,仔细解答.
分析:平面α、β和不在这两个平面内的两直线m、n:若α⊥β,m⊥n,m∥α,则n∥β或n与β相交;若α⊥β,m∥n,m∥α,则n∥β或n与β相交;若α∥β,m⊥α,则m⊥β,若m∥n,则n⊥β;若α∥β,m⊥α,则m⊥β,若m⊥n,则n∥β.
解答:平面α、β和不在这两个平面内的两直线m、n,
命题1:若α⊥β,m⊥n,m∥α,则n∥β或n与β相交,故命题1不正确;
命题2:若α⊥β,m∥n,m∥α,则n∥β或n与β相交,命题2不正确;
命题3:若α∥β,m⊥α,则m⊥β;若m∥n,则n⊥β,故命题3正确;
命题4:若α∥β,m⊥α,则m⊥β;若m⊥n,则n∥β,故命题4正确.
故选C.
点评:本题考查平面的基本性质及推论,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
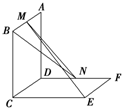 如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M、N分别为AB、DF的中点,求证:直线ME与BN是两条异面直线.
如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M、N分别为AB、DF的中点,求证:直线ME与BN是两条异面直线.