题目内容
已知函数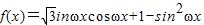 的周期为2π,其中ω>0.
的周期为2π,其中ω>0.(I)求ω的值及函数f(x)的单调递增区间;
(II)在△ABC中,设内角A、B、C所对边的长分别为a、b,c若a=
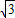 ,c=2,f(A)=
,c=2,f(A)= ,求b的值.
,求b的值.
【答案】分析:(I)先化简函数,利用周期为2π,可求w的值,从而可得函数f(x)的单调递增区间;
(II)由f(A)= ,求得A的值,再由余弦定理,即可求b的值.
,求得A的值,再由余弦定理,即可求b的值.
解答:解:(I)函数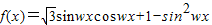 =
=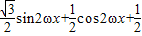 =sin(2ω+
=sin(2ω+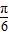 )+
)+
∵T=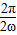 =2π,∴ω=
=2π,∴ω=
∴f(x)=sin(x+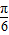 )+
)+
∴函数f(x)的单调递增区间为[2kπ-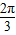 ,2kπ+
,2kπ+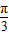 ],k∈Z;
],k∈Z;
(II)∵f(x)=sin(x+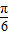 )+
)+
∴f(A)=sin(A+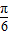 )+
)+ =
=
∴sin(A+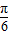 )=1
)=1
∵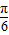 <A+
<A+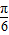 <
<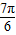
∴A+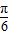 =
=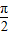
∴A=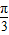
由余弦定理:a2=b2+c2-2bccosA
∴b2+4-2b=3
∴b=1.
点评:本题考查三角函数的化简,考查余弦定理的运用,考查学生的计算能力,属于中档题.
(II)由f(A)=
 ,求得A的值,再由余弦定理,即可求b的值.
,求得A的值,再由余弦定理,即可求b的值.解答:解:(I)函数
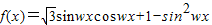 =
=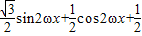 =sin(2ω+
=sin(2ω+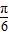 )+
)+
∵T=
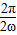 =2π,∴ω=
=2π,∴ω=
∴f(x)=sin(x+
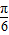 )+
)+
∴函数f(x)的单调递增区间为[2kπ-
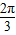 ,2kπ+
,2kπ+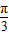 ],k∈Z;
],k∈Z;(II)∵f(x)=sin(x+
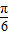 )+
)+
∴f(A)=sin(A+
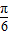 )+
)+ =
=
∴sin(A+
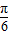 )=1
)=1∵
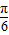 <A+
<A+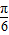 <
<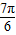
∴A+
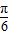 =
=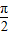
∴A=
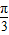
由余弦定理:a2=b2+c2-2bccosA
∴b2+4-2b=3
∴b=1.
点评:本题考查三角函数的化简,考查余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 的周期为2,当
的周期为2,当 时,
时,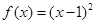 ,如果
,如果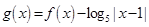 则函数
则函数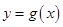 的所有零点之和为:
的所有零点之和为: 的周期为2,当
的周期为2,当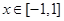 时
时 ,那么函数
,那么函数 的图象的交点共有( )
的图象的交点共有( )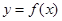 的周期为2,当
的周期为2,当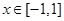 时
时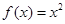 ,那么函数
,那么函数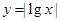 的图象的交点共有
的图象的交点共有 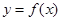 的周期为2,当
的周期为2,当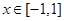 时
时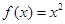 ,那么函数
,那么函数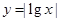 的图象的交点共有
的图象的交点共有