题目内容
【题目】设 
，g（x）=ax+5﹣2a（a＞0）．
（1）求f（x）在x∈[0，1]上的值域；
（2）若对于任意x1∈[0，1]，总存在x0∈[0，1]，使得g（x0）=f（x1）成立，求a的取值范围．
【答案】
（1）解：法一：（导数法） 
在x∈[0，1]上恒成立．
∴f（x）在[0，1]上增，
∴f（x）值域[0，1]．
法二：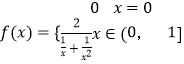 
，用复合函数求值域．
法三： 
用双勾函数求值域．
（2）解：f（x）值域[0，1]，g（x）=ax+5﹣2a（a＞0）在x∈[0，1]上的值域[5﹣2a，5﹣a]．
由条件，只须[0，1][5﹣2a，5﹣a]．
∴ 
【解析】（1）求f（x）的值域问题可用导数法；注意到分母为x2 ， 可分子分母同除以x2 ， 将分母变为关于 
的二次函数解决； 还可以将分母换元，转化为用双钩函数求最值．（2）对于任意x1∈[0，1]，f（x1）范围由（1）可知，由题意即g（x）的值域包含f（x）的值域，转化为集合的关系问题．
【考点精析】根据题目的已知条件，利用函数的值域的相关知识可以得到问题的答案，需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．
练习册系列答案
全程金卷系列答案
相关题目
