题目内容

已知（sinx-2cosx）（3+2sinx+2cosx）=0，则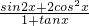 $数学公式$ 的值为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

C
分析：通过方程求出tanx=2，然后求出cos²x的值，求出sin2x的值，即可求出表达式的值．
解答：由（sinx-2cosx）（3+2sinx+2cosx）=0可得 sinx-2cosx=0 或者 sinx+cosx=- $\text{[math]}$
可因为（sinx+cosx）的最小值为 $\text{[math]}$ ＞- $\text{[math]}$ ，故sinx+cosx=- $\text{[math]}$ 舍去即sinx-2cosx=0 所以sinx=2cosx 所以tanx=2 所以1=sin²x+cos²x=5cos²x，故cos²x= $\text{[math]}$ ，
所以sin2x=2sinx•cosx=2×2cosx•cosx=4cos²x= $\text{[math]}$
所以 $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
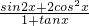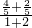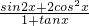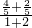故选C．
点评：本题是基础题，考查三角函数的化简求值，考查计算能力，注意公式的灵活应用．

练习册系列答案

实验班小学毕业总复习系列答案

口算加应用题专项天天练系列答案

小学毕业升学学业水平测试系列答案

小考专家系列答案

夺冠百分百中考冲刺系列答案

易杰教育中考解读系列答案

初中新课标阅读系列答案

状元阅读系列答案

金钥匙1加1小升初总复习系列答案

文言文图解注释系列答案

相关题目

给出下列命题，其中正确命题的个数为（　　）
①在区间（0，+∞）上，函数y=x^-1，y=x

，y=（x-1）²，y=x³中有三个是增函数；
②命题p：?x∈R，sinx≤1．则￢p：?x₀∈R，使sinx₀＞1；
③若函数f（x）是偶函数，则f（x-1）的图象关于直线x=1对称；
④已知函数f（x）=

log3(x-1)，x＞2

则方程f（x）=

有2个实数根．

（2013•成都一模）已知

=3，则tanx的值是（　　）

（2012•许昌三模）已知函数f（x）=sinx+cosx，g（x）=sinx-cosx，下列四个命题：
①将f（x）的图象向右平移

个单位可得到g（x）的图象；
②y=f（x）g（x）是偶函数；
③f（x）与g（x）均在区间[-

]上单调递增；
④y=

的最小正周期为2π．
其中真命题的个数是（　　）

（2012•许昌三模）已知函数f（x）=sinx+cosx，g（x）=sinx-cosx，下列四个命题：
①将f（x）的图象向右平移

个单位可得到g（x）的图象；
②y=f（x）g（x）是偶函数；
③y=

是以π为周期的周期函数；
④对于?x₁∈R，?x₂∈R，使f（x₁）＞g（x₂）．
其中真命题的个数为（　　）

已知下列命题四个命题：
①函数y=sin(

-2x)的单调递增区间是[kπ-

](k∈Z)；
②若x是第一象限的角，则y=sinx是增函数；
③α，β∈(0，

)，且cosα＜sinβ，则α+β＞

；
④若sinx+siny=

，则siny-cos²x的最大值是

．
其中真命题的个数有（　　）