题目内容
已知向量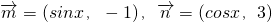 .
.
(1)当 时,求
时,求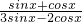 的值;
的值;
(2)设函数f(x)=(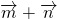 )•
)• ,求f(x)的单调增区间;
,求f(x)的单调增区间;
(3)已知在锐角△ABC中,a,b,c分别为角A,B,C的对边, c=2asin(A+B),对于(2)中的函数f(x),求f(B+
c=2asin(A+B),对于(2)中的函数f(x),求f(B+ )的取值范围.
)的取值范围.
解:(1)∵向量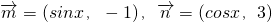 ,
,
∴3sinx=-cosx,
∴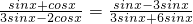 =-
=- ;
;
(2)函数f(x)=(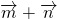 )•
)• =(sinx+cosx,2)•(sinx,-1)=sin2x+sinxcosx-2
=(sinx+cosx,2)•(sinx,-1)=sin2x+sinxcosx-2
= +
+ sin2x-2=
sin2x-2= sin(
sin(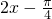 )-
)-
由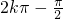 ≤
≤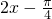 ≤
≤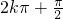 ,可得
,可得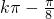 ≤x≤
≤x≤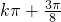
∴f(x)的单调增区间为[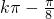 ,
,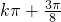 ](k∈Z);
](k∈Z);
(3)∵ c=2asin(A+B),
c=2asin(A+B),
∴ sinC=2sinAsinC,
sinC=2sinAsinC,
∴sinA=
∵A∈(0,π),∴A=
∵△ABC为锐角三角形,∴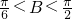
f(B+ )=
)= sin[2(B+
sin[2(B+ )-
)- ]-
]- =
= sin2B-
sin2B-
∵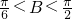 ,∴
,∴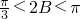
∴0<sin2B≤1
∴- <f(B+
<f(B+ )≤
)≤ -
- .
.
分析:(1)利用向量共线的条件,可得3sinx=-cosx,代入,即可得到结论;
(2)利用向量数量积公式化简函数,结合正弦函数的单调增区间,可得f(x)的单调增区间;
(3)求出A的值,确定B的范围,化简函数,可得函数的值域.
点评:本题考查向量知识的运用,考查三角函数的化简,考查学生分析解决问题的能力,属于中档题.
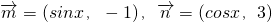 ,
,
∴3sinx=-cosx,
∴
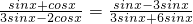 =-
=- ;
;(2)函数f(x)=(
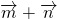 )•
)• =(sinx+cosx,2)•(sinx,-1)=sin2x+sinxcosx-2
=(sinx+cosx,2)•(sinx,-1)=sin2x+sinxcosx-2=
 +
+ sin2x-2=
sin2x-2= sin(
sin(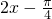 )-
)-
由
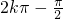 ≤
≤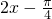 ≤
≤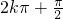 ,可得
,可得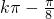 ≤x≤
≤x≤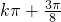
∴f(x)的单调增区间为[
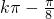 ,
,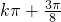 ](k∈Z);
](k∈Z);(3)∵
 c=2asin(A+B),
c=2asin(A+B),∴
 sinC=2sinAsinC,
sinC=2sinAsinC,∴sinA=

∵A∈(0,π),∴A=

∵△ABC为锐角三角形,∴
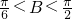
f(B+
 )=
)= sin[2(B+
sin[2(B+ )-
)- ]-
]- =
= sin2B-
sin2B-
∵
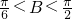 ,∴
,∴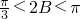
∴0<sin2B≤1
∴-
 <f(B+
<f(B+ )≤
)≤ -
- .
.分析:(1)利用向量共线的条件,可得3sinx=-cosx,代入,即可得到结论;
(2)利用向量数量积公式化简函数,结合正弦函数的单调增区间,可得f(x)的单调增区间;
(3)求出A的值,确定B的范围,化简函数,可得函数的值域.
点评:本题考查向量知识的运用,考查三角函数的化简,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 ,
,
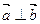 时,求
时,求 的取值集合;
的取值集合; 的单调递增区间 .
的单调递增区间 .  ,
,
 时,求函数f(x)的值域;
时,求函数f(x)的值域; 个单位后,再将所得图象上各点向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的图象与直线
个单位后,再将所得图象上各点向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的图象与直线 以及x轴所围成的封闭图形的面积.
以及x轴所围成的封闭图形的面积.

 ,
,
 时,求函数
时,求函数 的值域:
的值域: 中,
中, 分别为角
分别为角 的对边,若
的对边,若 ,求边
,求边 .
. ,
,
 时,求
时,求 的取值集合; (2)求函数
的取值集合; (2)求函数 的单调递增区间
的单调递增区间