题目内容
已知:如图12,P是正方形ABCD所在平面外一点,PA=PB=PC=PD=a,AB=a.
求:平面APB与平面CPD相交所成较大的二面角的余弦值.

解析:
分析:为了找到二面角及其平面角,必须依据题目的条件,找出两个平面的交线.
解:因为 AB∥CD,CD ![]() 平面CPD,AB
平面CPD,AB ![]() 平面CPD.
平面CPD.
所以 AB∥平面CPD.
又 P∈平面APB,且P∈平面CPD,
因此 平面APB∩平面CPD=l,且P∈l.
所以 二面角B-l-C就是平面APB和平面CPD相交所得到的一个二面角.
因为 AB∥平面CPD,AB ![]() 平面APB,平面CPD∩平面APB=l,
平面APB,平面CPD∩平面APB=l,
所以 AB∥l.
过P作PE⊥AB,PE⊥CD.
因为 l∥AB∥CD,
因此 PE⊥l,PF⊥l,
所以 ∠EPF是二面角B-l-C的平面角.
因为 PE是正三角形APB的一条高线,且AB=a,
因为 E,F分别是AB,CD的中点,
所以 EF=BC=a.
在△EFP中,
![]()
![]()

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
(本小题共12分)
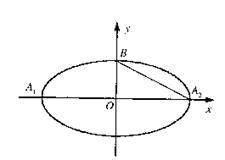
已知椭圆![]() A1、A2、B是椭圆的顶点(如图),直线
A1、A2、B是椭圆的顶点(如图),直线![]() 与椭圆交于异于椭圆顶点的P、Q两点,且
与椭圆交于异于椭圆顶点的P、Q两点,且![]() //A2B。若此椭圆的离心率为
//A2B。若此椭圆的离心率为![]()
(I)求此椭圆的方程;
|

 ,∠APB=∠ADB=60°
,∠APB=∠ADB=60°
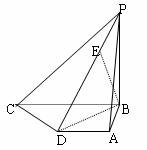 (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD; (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD;