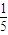题目内容
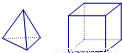
 正四面体各面分别标有数字1、2、3、4,正六面体各面分别标有数字1、2、3、4、5、6,同时掷这两个正多面体,并将它们朝下面上的数字相加.则两个正多面体朝下面上的数字之和是3的倍数的概率为
正四面体各面分别标有数字1、2、3、4,正六面体各面分别标有数字1、2、3、4、5、6,同时掷这两个正多面体,并将它们朝下面上的数字相加.则两个正多面体朝下面上的数字之和是3的倍数的概率为
- A.

- B.

- C.

- D.

B
分析:本题是2步实验,一步是6种情况,另一步是4种情况,用乘法原理可得出所有情况;利用树状图列举出所有情况,看两个正多面体朝下面上的数字之和是3的倍数的情况数,最后根据概率公式计算即可.
解答: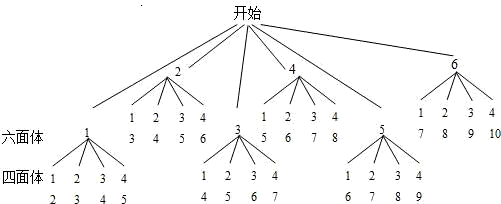 解:根据题意,用树状图列举出所有情况,可得共有24种情况,其中,和为3的倍数的情况是8种,
解:根据题意,用树状图列举出所有情况,可得共有24种情况,其中,和为3的倍数的情况是8种,
所以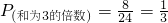 .
.
故选B.
点评:考查列树状图解决概率问题;找到两个正多面体朝下面上的数字之和是3的倍数的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情况数之比.
分析:本题是2步实验,一步是6种情况,另一步是4种情况,用乘法原理可得出所有情况;利用树状图列举出所有情况,看两个正多面体朝下面上的数字之和是3的倍数的情况数,最后根据概率公式计算即可.
解答:
 解:根据题意,用树状图列举出所有情况,可得共有24种情况,其中,和为3的倍数的情况是8种,
解:根据题意,用树状图列举出所有情况,可得共有24种情况,其中,和为3的倍数的情况是8种,所以
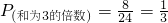 .
.故选B.
点评:考查列树状图解决概率问题;找到两个正多面体朝下面上的数字之和是3的倍数的情况数是解决本题的关键;用到的知识点为:概率等于所求情况数与总情况数之比.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 正四面体各面分别标有数字1、2、3、4,正六面体各面分别标有数字1、2、3、4、5、6,同时掷这两个正多面体,并将它们朝下面上的数字相加.则两个正多面体朝下面上的数字之和是3的倍数的概率为( )
正四面体各面分别标有数字1、2、3、4,正六面体各面分别标有数字1、2、3、4、5、6,同时掷这两个正多面体,并将它们朝下面上的数字相加.则两个正多面体朝下面上的数字之和是3的倍数的概率为( )