题目内容
已知偶函数f(x)(x∈R),当 时,f(x)= -x(2+x),当
时,f(x)= -x(2+x),当 时,f(x)=(x-2)(a-x)(
时,f(x)=(x-2)(a-x)(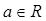 ).关于偶函数f(x)的图象G和直线
).关于偶函数f(x)的图象G和直线 :y=m(
:y=m( )的3个命题如下:
)的3个命题如下:
当a=2,m=0时,直线 与图象G恰有3个公共点;
与图象G恰有3个公共点;
当a=3,m= 时,直线
时,直线 与图象G恰有6个公共点;
与图象G恰有6个公共点; ,使得直线
,使得直线 与图象G交于4个点,且相邻点之间的距离相等.其中正确命题的序号是(A)
与图象G交于4个点,且相邻点之间的距离相等.其中正确命题的序号是(A)
A. ①② B. ①③ C. ②③ D. ①②③
A
解析试题分析:根据题意,由于偶函数f(x)(x∈R),当 时,f(x)= -x(2+x),当
时,f(x)= -x(2+x),当 时,f(x)=(x-2)(a-x)(
时,f(x)=(x-2)(a-x)(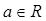 ),那么可知函数当a=2,m=0时,则可知
),那么可知函数当a=2,m=0时,则可知 时,f(x)=(x-2)(2-x)=-(2-x)
时,f(x)=(x-2)(2-x)=-(2-x) ,那么可知偶函数关于y轴对称,则可知偶函数f(x)的图象G和直线
,那么可知偶函数关于y轴对称,则可知偶函数f(x)的图象G和直线 :y=0(
:y=0( )的交点为3个,故命题1成立,对于,当a=3,m=
)的交点为3个,故命题1成立,对于,当a=3,m= 时,直线
时,直线 与图象G恰有6个公共点;成立,对于
与图象G恰有6个公共点;成立,对于 ,使得直线
,使得直线 与图象G交于4个点,且相邻点之间的距离相等,错误故选A.
与图象G交于4个点,且相邻点之间的距离相等,错误故选A.
考点:函数的性质
点评:主要是考查了函数性质的运用,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. | B. | C. | D. |
设函数 为奇函数,
为奇函数, 则
则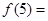 ( )
( )
| A.0 | B.1 | C. | D.5 |
三个数 的大小顺序是
的大小顺序是
| A.0.76<log0.76<60.7 | B.0.76<60.7<log0.76 |
| C.log0.76<60.7<0.76 | D. |
已知幂函数 的图象经过点(4,2),则
的图象经过点(4,2),则 ( )
( )
A.2 | B.4 | C.4 | D.8 |
定义域为R的函数 满足
满足 时,
时, 若
若 时,
时, 恒成立,则实数t的取值范围是
恒成立,则实数t的取值范围是
A. | B. |
C. | D. |
已知函数 ,则实数a的值等于 ( )
,则实数a的值等于 ( )
| A.-3 | B.-l | C.1 | D.-3或l |
设 =log36,b=log510,c=log714,则
=log36,b=log510,c=log714,则
| A.c>b>a | B.b>c>a |
| C.a>c>b | D.a>b>c |
 (
( )的图象如下面左图所示,则函数
)的图象如下面左图所示,则函数 的图象是( )
的图象是( )