题目内容
13. 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}AB$.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{{\sqrt{2}}}{2}AB$.(1)证明:BC1∥平面A1CD;
(2)求异面直线BC1和A1D所成角的大小;
(3)当AB=$2\sqrt{2}$时,求三棱锥C-A1DE的体积.
分析 (1)连接AC1与A1C相交于点F,连接DF,利用矩形的性质、三角形中位线定理可得:DF∥BC1,再利用线面平行的判定定理即可证明.
(2)由(1)可得∠A1DF或其补角为异面直线BC1和A1D所成角.不妨取AB=2,在△A1DF中,由余弦定理即可得出.
(3)利用面面垂直的性质定理可得:CD⊥平面ABB1A1,利用${S}_{△{A}_{1}DE}$=${S}_{矩形AB{B}_{1}{A}_{1}}$-S△BDE-${S}_{△{A}_{1}{B}_{1}E}$-${S}_{△A{A}_{1}D}$可得,再利用三棱锥C-A1DE的体积V=$\frac{1}{3}×CD×{S}_{△{A}_{1}DE}$即可得出.
解答 (1)证明:连接AC1与A1C相交于点F,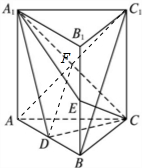 连接DF,
连接DF,
由矩形ACC1A1可得点F是AC1的中点,又D是AB的中点,
∴DF∥BC1,
∵BC1?平面A1CD,DF?平面A1CD,
∴BC1∥平面A1CD;
(2)解:由(1)可得∠A1DF或其补角为异面直线BC1和A1D所成角.不妨取AB=2,
$DF=\frac{1}{2}B{C}_{1}$═$\frac{1}{2}\sqrt{B{C}^{2}+{C}_{1}{C}^{2}}$=$\frac{1}{2}\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=1,
A1D=$\sqrt{{A}_{1}{A}^{2}+A{D}^{2}}$=$\sqrt{(\sqrt{2})^{2}+{1}^{2}}$=$\sqrt{3}$,
${A}_{1}F=\frac{1}{2}{A}_{1}C$=1.
在△A1DF中,由余弦定理可得:cos∠A1DF=$\frac{{1}^{2}+(\sqrt{3})^{2}-{1}^{2}}{2×1×\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∠A1DF∈(0,π),
∴∠A1DF=$\frac{π}{6}$,
∴异面直线BC1和A1D所成角的大小;
(3)解:∵AC=BC,D为AB的中点,
∴CD⊥AB,
∵平面ABB1A1∩平面ABC=AB,
∴CD⊥平面ABB1A1,
CD=$\sqrt{B{C}^{2}-B{D}^{2}}$=$\sqrt{2}$.
${S}_{△{A}_{1}DE}$=${S}_{矩形AB{B}_{1}{A}_{1}}$-S△BDE-${S}_{△{A}_{1}{B}_{1}E}$-${S}_{△A{A}_{1}D}$
=$2×2\sqrt{2}$-$\frac{1}{2}×\sqrt{2}×1$-$\frac{1}{2}×1×2\sqrt{2}$-$\frac{1}{2}×2×\sqrt{2}$=$\frac{3\sqrt{2}}{2}$,
∴三棱锥C-A1DE的体积V=$\frac{1}{3}×CD×{S}_{△{A}_{1}DE}$=$\frac{1}{3}×\sqrt{2}×\frac{3\sqrt{2}}{2}$=1.
点评 本题考查了直三棱柱的性质、矩形的性质、三角形中位线定理、线面平行的判定定理、异面直线所成角、余弦定理、勾股定理、线面面面垂直的性质定理、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

 已知在△ABC中,A、B、C对边分别为a、b、c,已知b=2$\sqrt{7}$,B=60°,a+c=10.
已知在△ABC中,A、B、C对边分别为a、b、c,已知b=2$\sqrt{7}$,B=60°,a+c=10.