题目内容
甲、乙、丙三个人依次参加摸奖活动，在一个不透明的摸奖箱中有六个同样大小、同样光滑的小球，每个小球标有一个编号，编号分别为1，2，3，4，5，6，活动规则是：每个人从这个摸奖箱中连续摸3次，每次摸一个球，每次摸完后，记下小球上的编号再将其放回箱中，充分搅拌后再进行下一次的摸取，三次摸完后将三个编号相加，若三个编号的和为4的倍数，则能得到一个纪念品，记获得纪念品的人数为X，则X的期望为
．
| 55 |
| 72 |
| 55 |
| 72 |
分析：根据随机变量X服从二项分布和求服从二项分布的变量的期望值公式，代入公式得到结果．
解答：解：三个编号和的取值范围是中的整数，其中4的倍数可能为4，8，12，16；
4的组合为（112），8的组合为（116）、（125）、（134）、（224）、（332），
12的组合为（156）、（246）、（336）、（345）、（552）、（444），
16的组合为（664）、（556）；
（ABC）结构的情况可出现6种，（AAB）结构的情况可出现3种，（AAA）结构的只有一种情况，则共有55种．
每个人获得纪念品的概率为
，
又X-B(3，
)，所以EX=
．
4的组合为（112），8的组合为（116）、（125）、（134）、（224）、（332），
12的组合为（156）、（246）、（336）、（345）、（552）、（444），
16的组合为（664）、（556）；
（ABC）结构的情况可出现6种，（AAB）结构的情况可出现3种，（AAA）结构的只有一种情况，则共有55种．
每个人获得纪念品的概率为
| 55 |
| 216 |
又X-B(3，
| 55 |
| 216 |
| 55 |
| 72 |
点评：本题考查二项分布与n次独立重复试验的模型，本题解题的关键是看出变量符合二项分布，这样题目的解题过程要简单的多．
练习册系列答案
相关题目
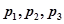，假设
互不相等，且假定各人能否完成任务的事件相互独立.
，其中
的一个排列，求所需派出人员数目
的分布列和均值（数学期望）
；
，试分析以怎样的先后顺序派出人员，可使所需派出的人员数目的均值（数学期望）达到最小，并证明之。
，假设
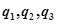，其中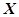
的分布列和均值（数字期望）
；
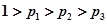，试分析以怎样的先后顺序派出人员，可使所需派出的人员数目的均值（数字期望）达到最小.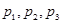
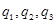，其中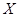
的分布列和均值（数字期望）
；
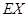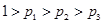，试分析以怎样的先后顺序派出人员，可使所需派出的人员数目的均值（数字期望）达到最小。