题目内容
函数f(x)=2x-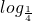 x-1,x∈[2,+∞)的值域 ________.
x-1,x∈[2,+∞)的值域 ________.
[ ,+∞)
,+∞)
分析:先对函数进行化简变形,分别判定每一个函数的单调性,根据两个增函数之和还是增函数得到函数的在[2,+∞)上的单调性,从而求出函数的值域.
解答:f(x)=2x-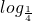 x-1=2x+log4x-1
x-1=2x+log4x-1
∵y=2x在[2,+∞)上单调递增
y=log4x在[2,+∞)上单调递增
∴f(x)=2x-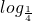 x-1=2x+log4x-1在[2,+∞)上单调递增
x-1=2x+log4x-1在[2,+∞)上单调递增
∴函数f(x)=2x-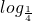 x-1,x∈[2,+∞)的值域[
x-1,x∈[2,+∞)的值域[ ,+∞)
,+∞)
故答案为:[ ,+∞)
,+∞)
点评:本题主要考查了指数函数、对数函数的值域,两个增函数之和还是增函数,属于基础题.
 ,+∞)
,+∞)分析:先对函数进行化简变形,分别判定每一个函数的单调性,根据两个增函数之和还是增函数得到函数的在[2,+∞)上的单调性,从而求出函数的值域.
解答:f(x)=2x-
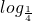 x-1=2x+log4x-1
x-1=2x+log4x-1∵y=2x在[2,+∞)上单调递增
y=log4x在[2,+∞)上单调递增
∴f(x)=2x-
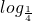 x-1=2x+log4x-1在[2,+∞)上单调递增
x-1=2x+log4x-1在[2,+∞)上单调递增∴函数f(x)=2x-
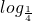 x-1,x∈[2,+∞)的值域[
x-1,x∈[2,+∞)的值域[ ,+∞)
,+∞)故答案为:[
 ,+∞)
,+∞)点评:本题主要考查了指数函数、对数函数的值域,两个增函数之和还是增函数,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=
,则满足f(x)=4的x的值是( )
|
| A、2 | B、16 |
| C、2或16 | D、-2或16 |