题目内容
设复数z的辐角主值为θ,θ∈(0,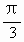 ),且满足|z-i|=1.
),且满足|z-i|=1.
(1)求复数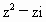 的辐角主值;
的辐角主值;
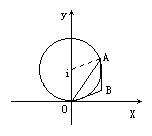
(2)设z,z-i在复平面上的对应点分别为A,B,求△OAB的面积S的取值范围.
答案:
解析:
解析:
|
解:(1)设z=r(cosθ+isinθ),∵|z-i|=1, ∴ ∴当θ∈ (2)由(1)知:|OA|=|z|=r=2sinθ;|OB|=|z-i|=1,且∠AOB=(θ+2π)- |

练习册系列答案
相关题目
设复数z=![]() ,则复数
,则复数![]() 的辐角主值为
的辐角主值为
[ ]
|
A. |
B. |
|
C. |
D. |
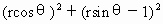 =1,∴r=2sinθ,∴z=sin2θ+
=1,∴r=2sinθ,∴z=sin2θ+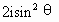 ,∴z-i=sin2θ+i
,∴z-i=sin2θ+i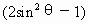 =sin2θ-icos2θ=cos
=sin2θ-icos2θ=cos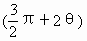 ,∴
,∴ -zi=z·(z-i)的辐角是
-zi=z·(z-i)的辐角是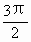 +3θ+2kπ(k∈Z).又因为θ∈
+3θ+2kπ(k∈Z).又因为θ∈ 的辐角主值为
的辐角主值为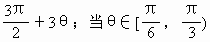 时,
时, .
.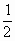 |OA|·|OB|·sin∠AOB=
|OA|·|OB|·sin∠AOB= =z(z为已知复数,z≠0)的三个根为
=z(z为已知复数,z≠0)的三个根为 ,若
,若 =1+i,那么
=1+i,那么 的辐角主值为
的辐角主值为


