题目内容
设
，则集合{x|x=f（n）}中元素个数是（ ）A．2
B．4
C．3
D．无穷多个
【答案】分析：依据两个复数代数形式的除法法则，化简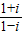
和
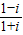，得到f（n）=in+（-i）n，分 n=4k，n=4k+1，
n=4k+2，n=4k+3这四种情况分别求出f（n）=的值，即得结论．
解答：解：∵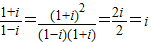
，∴
，
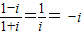根据虚数单位i的幂运算性质，有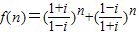
=in+（-i）n=
，
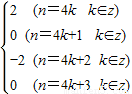故f（n）有3个不同的值，
故选 C．
点评：本题考查复数代数形式的混合运算，虚数单位i的幂运算性质，体现了分类讨论的数学思想，分类讨论是解题的难点．
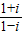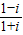和，得到f（n）=in+（-i）n，分 n=4k，n=4k+1，n=4k+2，n=4k+3这四种情况分别求出f（n）=的值，即得结论．
解答：解：∵
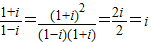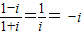，∴，根据虚数单位i的幂运算性质，有
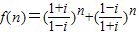=in+（-i）n=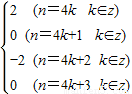，故f（n）有3个不同的值，
故选 C．
点评：本题考查复数代数形式的混合运算，虚数单位i的幂运算性质，体现了分类讨论的数学思想，分类讨论是解题的难点．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
，则集合{x|x＝f(n)}中元素的个数是
，则集合{x|x=f（n）}中元素个数是（ ）
，则集合{x|x=f（n）}中元素个数是（ ）