Question

(理)从6名男同学和4名女同学中随机选出3名同学参加一项测试,每位同学通过测试的概率都为.试求:

(1)选出的三位同学中,至少有一名女同学的概率;

(2)选出的三位同学中,同学甲被选中并且通过测试的概率;

(3)设选出的三位同学中男同学的人数为ξ,求ξ的分布列和数学期望.

(文)某人抛掷一枚硬币,出现正面、反面的概率均为.构造数列{a_n},使得a_n=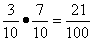,记S_n=a₁+a₂+…+a_n(n∈N^*).

(1)求S₄=2的概率;

(2)若前两次均出现正面,求2≤S₆≤4的概率.

Answer 1

答案：(理)解:(1)P=1.

(2)甲被选中的概率为,∴甲被选中且通过测试的概率为.

(3)ξ的取值为0、1、2、3,

P(ξ=0)=,P(ξ=1)=,

P(ξ=2)=,P(ξ=3)=,

∴ξ的分布列为

ξ	0	1	2	3
P

∴Eξ=+1+=.

(文)解：(1)若S₄=2,则需4次中有3次正面1次反面,设概率为P₁,则P₁=()³()=4()⁴=,∴S₄=2的概率为.

(2)∵2≤S₆≤4且前两次出现正面,则后4次中有2次正面2次反面或3次正面1次反面,设其概率为P₂,则P₂=××()²()²+××()³=,∴若前两次均出现正面,则2≤S₆≤4的概率为.