题目内容
已知直线l:(2l+1)x+(l+2)y+2l+2=0(l∈R),有下列四个结论:
①直线l经过定点(0,-2);
②若直线l在x轴和y轴上的截距相等,则l=1;
③当l∈[1, 4+3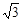 ]时,直线l的倾斜角q∈[120°,135°];
]时,直线l的倾斜角q∈[120°,135°];
④当l∈(0,+∞)时,直线l与两坐标轴围成的三角形面积的最小值为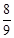 .
.
其中正确结论的是 (填上你认为正确的所有序号).
【答案】
②④
【解析】①因为直线l: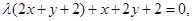 由
由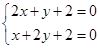 得
得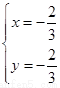 ,
,
所以直线l恒过定点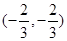 ,错;②若直线l在x轴和y轴上的截距相等,则其斜率为-1,所以
,错;②若直线l在x轴和y轴上的截距相等,则其斜率为-1,所以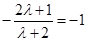 ,所以l=1.正确.③因为直线l的斜率
,所以l=1.正确.③因为直线l的斜率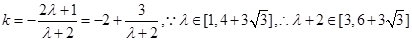 ,
,
所以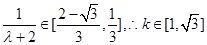 ,显然直线l的倾斜角q
,显然直线l的倾斜角q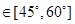 ,错.
,错.
④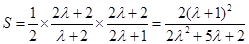 ,
,
设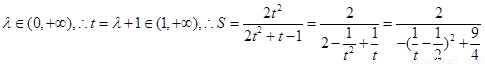 ,
,
当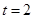 时,S取得最小值,最小值为
时,S取得最小值,最小值为 .正确.
.正确.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ]时,直线l的倾斜角q∈[120°,135°];
]时,直线l的倾斜角q∈[120°,135°]; .
.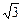 ]时,直线l的倾斜角q∈[120°,135°];
]时,直线l的倾斜角q∈[120°,135°]; .
.