题目内容
设集合M＝{x|m≤x≤m＋
}，N＝{x|n－
≤x≤n}且M，N都是集合{x|0≤x≤1}的子集，如果把b－a叫做集合{x|a≤x≤b}的“长度”，那么集合M∩N的“长度”的最小值是
[ ]
A．
B．
C．
D．
答案：C
解析：
解析：
|
由题意知 ∴ 同理，0≤m≤ 借助数轴可知M∩N的长度在n＝1，m＝0时，有最小“长度”值为 |
≤n≤1．
．
＝
．
练习册系列答案
相关题目
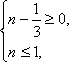
M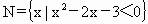
，集合M∩N等于