题目内容
设P是椭圆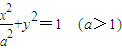 短轴的一个端点,Q为椭圆上一个动点,求|PQ|的最大值.
短轴的一个端点,Q为椭圆上一个动点,求|PQ|的最大值.
【答案】分析:依题意可知|PQ|= ,因为Q在椭圆上,所以x2=a2(1-y2),|PQ|2=a2(1-y2)+y2-2y+1=(1-a2)y2-2y+1+a2
,因为Q在椭圆上,所以x2=a2(1-y2),|PQ|2=a2(1-y2)+y2-2y+1=(1-a2)y2-2y+1+a2
=(1-a2)(y- )2-
)2- +1+a2.由此分类讨论进行求解.
+1+a2.由此分类讨论进行求解.
解答:解:由已知得到P(0,1)或P(0,-1)
由于对称性,不妨取P(0,1)
设Q(x,y)是椭圆上的任一点,
则|PQ|= ,①
,①
又因为Q在椭圆上,
所以,x2=a2(1-y2),
|PQ|2=a2(1-y2)+y2-2y+1=(1-a2)y2-2y+1+a2
=(1-a2)(y- )2-
)2- +1+a2.②
+1+a2.②
因为|y|≤1,a>1,若a≥ ,则|
,则| |≤1,
|≤1,
所以如果它包括对称轴的x的取值,那么就是顶点上取得最大值,
即当-1≤ ≤1时,
≤1时,
在y= 时,|PQ|取最大值
时,|PQ|取最大值 ;
;
如果对称轴不在y的取值范围内的话,那么根据图象给出的单调性来求解.
即当 <-1时,则当y=-1时,|PQ|取最大值2.
<-1时,则当y=-1时,|PQ|取最大值2.
点评:本题考查椭圆的基本性质及其应用,解题时要认真审题,细心计算.
 ,因为Q在椭圆上,所以x2=a2(1-y2),|PQ|2=a2(1-y2)+y2-2y+1=(1-a2)y2-2y+1+a2
,因为Q在椭圆上,所以x2=a2(1-y2),|PQ|2=a2(1-y2)+y2-2y+1=(1-a2)y2-2y+1+a2=(1-a2)(y-
 )2-
)2- +1+a2.由此分类讨论进行求解.
+1+a2.由此分类讨论进行求解.解答:解:由已知得到P(0,1)或P(0,-1)
由于对称性,不妨取P(0,1)
设Q(x,y)是椭圆上的任一点,
则|PQ|=
 ,①
,①又因为Q在椭圆上,
所以,x2=a2(1-y2),
|PQ|2=a2(1-y2)+y2-2y+1=(1-a2)y2-2y+1+a2
=(1-a2)(y-
 )2-
)2- +1+a2.②
+1+a2.②因为|y|≤1,a>1,若a≥
 ,则|
,则| |≤1,
|≤1,所以如果它包括对称轴的x的取值,那么就是顶点上取得最大值,
即当-1≤
 ≤1时,
≤1时,在y=
 时,|PQ|取最大值
时,|PQ|取最大值 ;
;如果对称轴不在y的取值范围内的话,那么根据图象给出的单调性来求解.
即当
 <-1时,则当y=-1时,|PQ|取最大值2.
<-1时,则当y=-1时,|PQ|取最大值2.点评:本题考查椭圆的基本性质及其应用,解题时要认真审题,细心计算.

练习册系列答案
相关题目