题目内容
| 某学校高三年级有学生1 000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学, (Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学; (Ⅱ)测得该年级所抽查的100名同学身高(单位:厘米)频率分布直方图如下图: | ||||||||||||||||
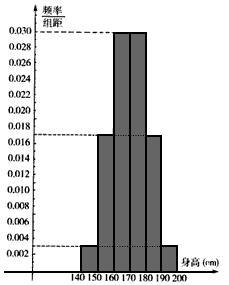 | ||||||||||||||||
| (ⅰ)统计方法中,同一组数据常用该组区间的中点值(例如区间[160,170)的中点值为165)作为代表。据此,计算这100名学生身高数据的期望μ及标准差σ(精确到0.1): (ⅱ)若总体服从正态分布,以样本估计总体,据此,估计该年级身高在(158.6,181.4)范围中的学生的人数; (Ⅲ)如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表: | ||||||||||||||||
|
体育锻炼与身高达标2×2列联表 | ||||||||||||||||
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系? 参考公式:  , ,参考数据: | ||||||||||||||||
 |
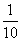 ,
,且事件“甲同学被抽到”与事件“乙同学被抽到”相互独立,
故甲、乙两人都被抽到的概率为
 。
。(Ⅱ)(ⅰ)总体数据的期望约为:
μ=145×0.03+155×0.17+165×0.30+175×0.30+185×0.17+195×0.03=170(cm),
标准差σ=11.4。
(ⅱ)由于μ=170,σ≈11.4,
当身高x∈(158.6,181.4)时,即x∈(μ-σ,μ+σ),
故身高落在(158.6,181.4)中的概率为0.682 6,
故身高落在(158.6,181.4)中的人数为683人。
(Ⅲ)(ⅰ)
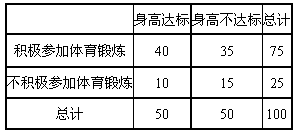
(ⅱ)
 ,
,故有75%把握认为体育锻炼与身高达标有关系。

(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
(Ⅱ)测得该年级所抽查的100名同学身高(单位:厘米)频率分布直方图如右图:
(ⅰ)统计方法中,同一组数据常用该组区间的中点值(例如区间[160,170)的中点值为165)作为代表.据此,计算这100名学生身高数据的期望μ及标准差φ(精确到0.1);
(ⅱ)若总体服从正态分布,以样本估计总体,据此,估计该年级身高在(158.6,181.4)范围中的学生的人数.
(Ⅲ)如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| 身高达标 | 身高不达标 | 总计 | |
| 积极参加体育锻炼 | 40 | ||
| 不积极参加体育锻炼 | 15 | ||
| 总计 | 100 |
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K2=
| π(ac-bd)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
(本小题满分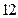 分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
分)某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
(Ⅰ)求甲、乙两同学都被抽到的概率,其中甲为A类同学,乙为B类同学;
(Ⅱ) 测得该年级所抽查的100名同学身高(单位:厘米) 频率分布直方图如右图:
(ⅰ) 统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为165)作为代表.据此,计算这100名学生身高数据的期望
的中点值为165)作为代表.据此,计算这100名学生身高数据的期望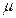 及标准差
及标准差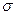 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,据此,估计该年级身高在 范围中的学生的人数.
范围中的学生的人数.
(Ⅲ) 如果以身高达170cm作为达标的标准,对抽取的100名学生,得到下列联表:
体育锻炼与身高达标2×2列联表
| | 身高达标 | 身高不达标 | 总计 |
| 积极参加体育锻炼 | 40 | | |
| 不积极参加体育锻炼 | | 15 | |
| 总计 | | | 100 |
(ⅱ)请问有多大的把握认为体育锻炼与身高达标有关系?
参考公式:K
 =
=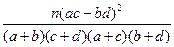 ,参考数据:
,参考数据:P(K  k) k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
(本题12分)
某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按 A类、B类分二层)从该年级的学生中共抽查100名同学,如果以身高达165cm作为达标的标准,对抽取的100名学生,得到以下列联表:
体育锻炼与身高达标2×2列联表
|
|
身高达标 |
身高不达标 |
总计 |
|
积极参加 体育锻炼 |
40 |
|
|
|
不积极参加 体育锻炼 |
|
15 |
|
|
总计 |
|
|
100 |
(1)完成上表;
(2)请问有多大的把握认为体育锻炼与身高达标有关系(K2值精确到0.01)?
参考公式:K2=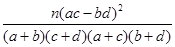 ,参考数据:
,参考数据:
|
P(K2≥k0) |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
|
K0 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称
为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中抽查100名同学.
(Ⅰ)求抽取的100名同学中,有多少名A 类同学?
(Ⅱ)如果以身高达到170厘米作为达标的标准,对抽取的100名学生进行统计,得到2×2列联表如下:
体育锻炼与身高达标2×2列联表
| 身高达标 | 身高不达标 | 总计 | |
| 积极参加体育锻炼 | 40 | 35 | 75 |
| 不积极参加体育锻炼 | 10 | 15 | 25 |
| 总计 | 50 | 50 | 100 |
请问是否有99%以上的把握认为体育锻炼与身高达标有关系?.
参考公式:K![]() =
=![]() ,
,
参考数据:
| P(K | 0.25 | 0.15 | 0.10 | 0.05 | 0 | 0.010 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |