题目内容
对于任意的四棱锥，平面α与其四条侧棱都相交且截面是平行四边形，符合上述条件的平面α共有（ ）个．
分析：如下图所示：要使截面四边形A1B1C1D1是平行四边形，我们只要证明A1B1∥C1D1，同时A1D1∥B1C1即可，根据侧面PAD与侧面PBC相交，侧面PAB与侧面PCD相交，利用面面平行的性质定理，我们易得结论．
解答：
证明：已知四棱锥P-ABCD，如图所示：
由侧面PAD与侧面PBC相交，侧面PAB与侧面PCD相交，
设两组相交平面的交线分别为m，n，
由m，n决定的平面为β，
作α与β平行且与四条侧棱相交，
则由面面平行的性质定理得截面必为平行四边形．
显然与β平行且与四棱锥的四条侧棱相交的平面α可作无数个，
故选D．
证明：已知四棱锥P-ABCD，如图所示：由侧面PAD与侧面PBC相交，侧面PAB与侧面PCD相交，
设两组相交平面的交线分别为m，n，
由m，n决定的平面为β，
作α与β平行且与四条侧棱相交，
则由面面平行的性质定理得截面必为平行四边形．
显然与β平行且与四棱锥的四条侧棱相交的平面α可作无数个，
故选D．
点评：判断线与线、线与面、面与面之间的关系，可将线线、线面、面面平行（垂直）的性质互相转换，进行证明，也可将题目的中直线放在空间正方体内进行分析．
练习册系列答案
相关题目
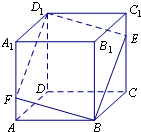如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．则下列命题中假命题是（ ）
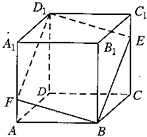如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．给出下列四个结论：