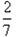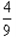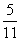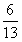Question

某班级要从5名男生，3名女生中选派4人参加某次社区服务，如果要求至少有一名女生，那么选派的4人中恰好有2名女生的概率为

6

13

．

Answer 1

分析：根据题意，首先计算从8人中任取4人的取法数目，再计算其中其中没有女生参加即全部为男生的取法数目，即可得选派的4人中至少有一名女生的取法的情况数目，进而计算选派的4人中有2名女生即2男2女的取法数目，由等可能事件的概率公式计算可得答案．

解答：解：根据题意，从8人中任取4人，有C₈⁴种取法，但其中没有女生参加即全部为男生的有C₅⁴种，则至少有一名女生的取法有C₈⁴-C₅⁴=65种；
其中恰有2名女生即2男2女的取法有C₅²×C₃²=30种；
则选派的4人中恰好有2名女生的概率为

30

65

=

6

13

；
故答案为

6

13

．

点评：本题考查概率的计算，涉及排列组合的应用，解题的难点在于运用排列组合的知识，计算“至少有一名女生”与“选派的4人中恰好有2名女生”的情况数目．