题目内容
(本题满分10分)已知函数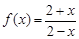 .
.
(I)试比较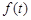 与
与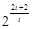
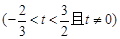 的大小;
的大小;
(II)设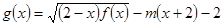 ,是否存在实数
,是否存在实数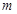 使得
使得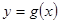 有零点?若存在,求出实数
有零点?若存在,求出实数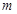 的取值范围;若不存在,请说明理由
的取值范围;若不存在,请说明理由
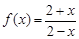 .
.(I)试比较
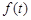 与
与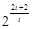
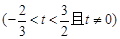 的大小;
的大小;(II)设
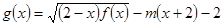 ,是否存在实数
,是否存在实数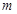 使得
使得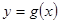 有零点?若存在,求出实数
有零点?若存在,求出实数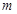 的取值范围;若不存在,请说明理由
的取值范围;若不存在,请说明理由(I)先求出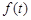 的范围为
的范围为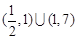
当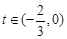 时,
时,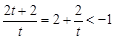 ,
,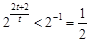 ,所以
,所以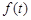
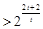 .
.
当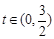 时,
时, ,
,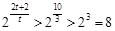 ,所以
,所以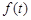
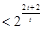 . 5分
. 5分
(II)
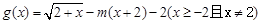
令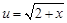 ,则
,则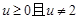 ,即方程
,即方程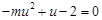 在
在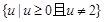 内有解,
内有解,
又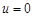 不满足,所以在
不满足,所以在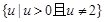 内有解,
内有解, ,利用两边范围一样,得
,利用两边范围一样,得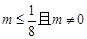 ,所以当
,所以当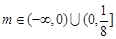 时
时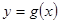 有零点. 10分
有零点. 10分
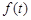 的范围为
的范围为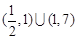
当
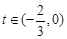 时,
时,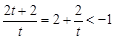 ,
,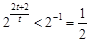 ,所以
,所以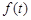
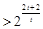 .
.当
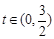 时,
时, ,
,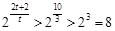 ,所以
,所以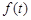
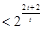 . 5分
. 5分(II)

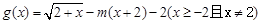
令
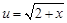 ,则
,则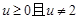 ,即方程
,即方程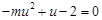 在
在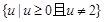 内有解,
内有解,又
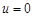 不满足,所以在
不满足,所以在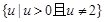 内有解,
内有解, ,利用两边范围一样,得
,利用两边范围一样,得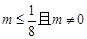 ,所以当
,所以当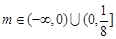 时
时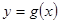 有零点. 10分
有零点. 10分略

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
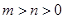 ,那么下列不等式成立的是
,那么下列不等式成立的是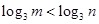
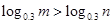
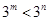
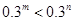
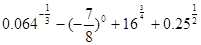 (2) 若
(2) 若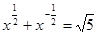 , 求
, 求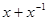 的值
的值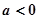 ,则函数
,则函数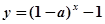 的图象必过点 ( )
的图象必过点 ( )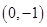
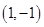
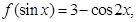 则
则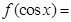
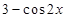
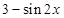
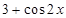
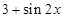
 的题号为
的题号为 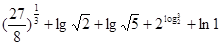 =
= 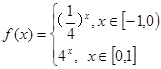 则
则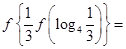
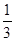
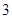
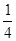
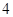
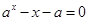 有两个实数解,则
有两个实数解,则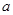 的取值范围是
的取值范围是