Question

若一个三棱锥的一条棱长为x，其余棱长为2，则x的取值范围是（　　）

• A．（0，

  3

  ）
• B．（0，

  6

  ）
• C．（0，2

  3

  ）
• D．（

  3

  ，2

  3

  ）

Answer 1

分析：由题设条件，设AB=AD=AC=BC=BD=2，DC=x，取AB的中点O，连接DO，CO，则CO⊥AB，DO⊥AB，CO=DO=

3

，由此能求出x的取值范围．

解答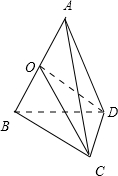：解：由题设条件，设AB=AD=AC=BC=BD=2，
DC=x，
取AB的中点O，连接DO，CO，
则CO⊥AB，DO⊥AB，
CO=DO=

4-1

=

3

，
∵△ODC中，OD，OC两边之差小于第三边DC，OD，OC两边之和大于第三边DC，
∴0＜x＜2

3

．
故选C．

点评：本题考查棱锥的结构特征，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．