题目内容
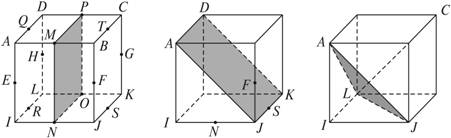
如图，正方体有8个顶点和12条棱，每条棱上均有一个中点，于是有棱的中点12个，顶点与中点合起来共有20个〔图(1)〕.过其中的两点可作一条直线；过其中不在同一直线上的三点可作一个平面.现在考虑这些直线与平面的垂直关系.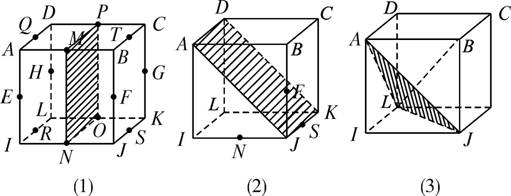
(1)试举出一直线与一平面相互垂直的例子(不少于4例)；
(2)若一直线与一平面相互垂直，我们就说这条直线与这个平面构成了一个“垂直关系组”，两个“垂直关系组”当且仅当其中两条直线和两个平面不全同一时称为相异的(或不同的).试求与正方体的棱相关的“垂直关系组”的个数.
【探究】 在正方体中，所有的棱都和与它相交的面垂直，利用中点也可产生与棱垂直的面.
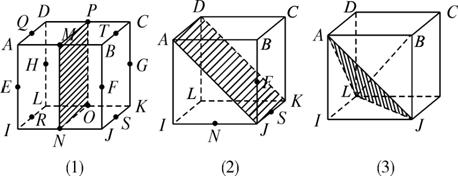
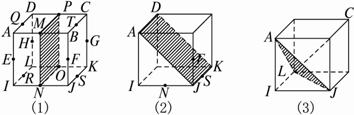
(1)例如AB⊥平面BCKJ〔如图(1)〕；
例如EF⊥平面MPON〔如图(1)〕；
例如NF⊥平面ADKJ〔如图(2)〕；
例如IC⊥平面AJL〔如图(3)〕.
(2)正方体的棱有12条，而每一条棱都与3个平面垂直，如图(1)中棱IJ与平面ID、平面NP及平面JC都垂直，所以与正方体的棱相关的“垂直关系组”的个数是12×3=36.
【规律总结】 挖掘正方体本身潜藏的特征，将每一条棱的情况分析清楚，做到不重不漏.
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
