题目内容
2.已知命题P:函数f(x)=lg(x2-ax+1)的定义域为R;命题q:?m∈[-2,3],使不等式a2-5a+5≥$\sqrt{{m}^{2}+1}$成立.(1)若命题p是真命题,求实数a的取值范围.
(2)若命题¬q是真命题,求实数a的取值范围.
(3)如果命题“p∨q”为真命题,且“p∧q”为假命题,求实数a的取值范围.
分析 (1)若命题p是真命题,转化为判别式△<0,解不等式即可求实数a的取值范围.
(2)若命题¬q是真命题,转化为不等式恒成立,即可求实数a的取值范围.
(3)如果命题“p∨q”为真命题,且“p∧q”为假命题,则p,q一真一假,建立不等式关系即可求实数a的取值范围.
解答 解:(1)f(x) 的定义域为R⇒x2-ax+1>0对一切实数x恒成立⇒△=(-a)2-4<0⇒-2<a<2,
故命题p是真命题时,实数a的取值范围是(-2,2);
(2)若命题¬q为真,则?m∈[-2,3],使a2-5a+5<$\sqrt{{m}^{2}+1}$恒成立.因为m∈[-2,3],
所以$\sqrt{{m}^{2}+1}$∈[1,$\sqrt{10}$],满足a2-5a+5<1,
解得1<a<4.故实数a的取值范围是(1,4).
(3)命题“p∨q”为真命题,且“p∧q”为假命题,则p,q一真一假.
①当p真q假时,可得$\left\{{\begin{array}{l}{-2<a<2}\\{1<a<4}\end{array}}\right.$⇒1<a<2;
②当p假q真时,可得$\left\{\begin{array}{l}{a≥0或a≤-2}\\{a≥4或a≤1}\end{array}\right.$,解得a≤-2或a≥4.
综合①②可得a的取值范围是(-∞,-2]∪(1,2)∪[4,+∞).
点评 本题主要考查命题的真假应用,根据复合命题真假之间的关系进行转化是解决本题的关键.

练习册系列答案
相关题目
12.设D为△ABC所在平面内一点,$\overrightarrow{BC}$=3$\overrightarrow{CD}$,则( )
| A. | $\overrightarrow{AD}$=-$\frac{1}{3}$$\overrightarrow{AC}$+$\frac{4}{3}$$\overrightarrow{AB}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{4}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{4}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{4}{3}$$\overrightarrow{AC}$-$\frac{1}{3}$$\overrightarrow{AB}$ |
13.已知f(x)=|lnx|,设0<a<b,且f(a)=f(b),则a+2b的取值范围是( )
| A. | [3,+∞) | B. | (3,+∞) | C. | $[2\sqrt{2},+∞)$ | D. | $(2\sqrt{2},+∞)$ |
10.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b>0)的渐近线和圆x2+y2-6y+8=0相切,则该双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | $\sqrt{3}$ |
11.x2+(y+2)2=3的圆心坐标、半径分别为( )
| A. | (0,2);3 | B. | (0,-2);3 | C. | $({0,2});\sqrt{3}$ | D. | $({0,-2});\sqrt{3}$ |
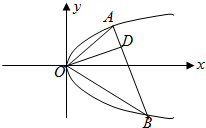 如图,已知直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1).
如图,已知直线与抛物线y2=2px(p>0)交于A、B两点,且OA⊥OB,OD⊥AB交AB于点D,点D的坐标为(2,1).