题目内容
已知椭圆 内有一点P(1,-1),F是椭圆的右焦点.
内有一点P(1,-1),F是椭圆的右焦点.(1)求该椭圆的离心率.
(2)在椭圆上求一点M,使得|MP|+2|MF|的值最小,并求出这个最小值.
【答案】分析:(1)根据椭圆的标准方程得到a2、b2的值,再由 求出c的值,再求出离心率;
求出c的值,再求出离心率;
(2)根据题意画出图形,利用椭圆的第二定义,把|MF|转化到右准线的距离,利用“两点间的距离最短”和条件,求出最小值以及对应的M点的坐标.
解答: 解:(1)依题设
解:(1)依题设
所以,离心率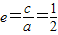
(2)如图:过M点作MQ垂直于椭圆的右准线,垂足为点Q,
由椭圆的第二定义和(1)可知:
 ,所以
,所以 ,
,
故|MP|+2|MF|=|MP|+|MQ|,
所以当P、M、Q三点共线时,由P(1,-1)得,
所求的值最小为|PQ|=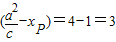 ,
,
把y=-1代入椭圆方程,解得x= 或x=-
或x=-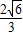 (舍去),
(舍去),
此时,M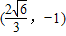 .
.
点评:本题考查了椭圆的简单性质应用,要求会根据椭圆的标准方程求出a、b、c、e的值,对于求距离的最值,一般利用第二定义把“椭圆上点到焦点的距离和到对应准线的距离”进行转化.
 求出c的值,再求出离心率;
求出c的值,再求出离心率;(2)根据题意画出图形,利用椭圆的第二定义,把|MF|转化到右准线的距离,利用“两点间的距离最短”和条件,求出最小值以及对应的M点的坐标.
解答:
 解:(1)依题设
解:(1)依题设
所以,离心率
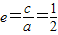
(2)如图:过M点作MQ垂直于椭圆的右准线,垂足为点Q,
由椭圆的第二定义和(1)可知:
 ,所以
,所以 ,
,故|MP|+2|MF|=|MP|+|MQ|,
所以当P、M、Q三点共线时,由P(1,-1)得,
所求的值最小为|PQ|=
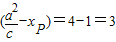 ,
,把y=-1代入椭圆方程,解得x=
 或x=-
或x=-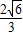 (舍去),
(舍去),此时,M
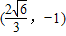 .
.点评:本题考查了椭圆的简单性质应用,要求会根据椭圆的标准方程求出a、b、c、e的值,对于求距离的最值,一般利用第二定义把“椭圆上点到焦点的距离和到对应准线的距离”进行转化.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 内有一点P
内有一点P ,以P为中点作弦MN,则直线MN的方程是( )
,以P为中点作弦MN,则直线MN的方程是( ) B.
B.
 D.
D.
 内有一点P(1,-1),F是椭圆的右焦点.
内有一点P(1,-1),F是椭圆的右焦点.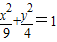 内有一点P(2,1),过点P作直线交椭圆于A、B两点.
内有一点P(2,1),过点P作直线交椭圆于A、B两点.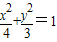 内有一点P(1,-1),F是椭圆的右焦点.
内有一点P(1,-1),F是椭圆的右焦点.