题目内容
设a∈R,则“a=-3”是“直线l1:ax+3y-1=0与直线l2:x+(a+2)y+4=0平行”的( )A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】分析:根据两条直线平行的条件列式,结合充分必要条件的判断进行正反推理,可得“a=-3”是“直线l1:ax+3y-1=0与直线l2:x+(a+2)y+4=0平行”的充分不必要条件.
解答:解:∵当a=-3时,直线l1:-3x+3y-1=0与直线l2:x-y+4=0显然平行;
∴“a=-3”是“直线l1:ax+3y-1=0与直线l2:x+(a+2)y+4=0平行”的充分条件
又∵若直线l1与直线l2平行,则有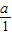 =
=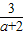 ,解之得a=1或a=-3,
,解之得a=1或a=-3,
∴反之不一定成立,故必要性不成立
故选:A
点评:本题给出两条直线,问a=-3是它们平行的什么条件,着重考查了两条直线位置关系的判断和充分必要条件的判断等知识,属于基础题.
解答:解:∵当a=-3时,直线l1:-3x+3y-1=0与直线l2:x-y+4=0显然平行;
∴“a=-3”是“直线l1:ax+3y-1=0与直线l2:x+(a+2)y+4=0平行”的充分条件
又∵若直线l1与直线l2平行,则有
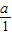 =
=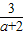 ,解之得a=1或a=-3,
,解之得a=1或a=-3,∴反之不一定成立,故必要性不成立
故选:A
点评:本题给出两条直线,问a=-3是它们平行的什么条件,着重考查了两条直线位置关系的判断和充分必要条件的判断等知识,属于基础题.

练习册系列答案
相关题目