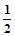题目内容
已知椭圆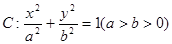 经过点
经过点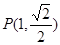 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)动直线 交椭圆
交椭圆 于
于 、
、 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得以
,使得以 为直径的圆恒过点
为直径的圆恒过点 .若存在,求出点
.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1)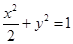 (2)点
(2)点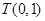 就是所求的点
就是所求的点
解析试题分析:(Ⅰ)椭圆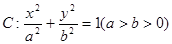 的两焦点与短轴的一个端点连线构成等腰直角三角形,所以
的两焦点与短轴的一个端点连线构成等腰直角三角形,所以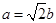 ,故椭圆的方程为
,故椭圆的方程为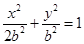 .
.
又因为椭圆经过点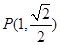 ,代入可得
,代入可得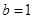 ,2分
,2分
所以 ,故所求椭圆方程为
,故所求椭圆方程为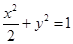 .4分
.4分
(Ⅱ)当直线 的斜率为0时,直线
的斜率为0时,直线 为
为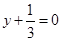 ,直线
,直线 交椭圆
交椭圆 于
于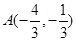 、
、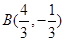 两点,以
两点,以 为直径的圆的方程为
为直径的圆的方程为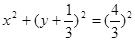 ;
;
当直线 的斜率不存在时,直线
的斜率不存在时,直线 为
为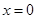 ,直线
,直线 交椭圆
交椭圆 于
于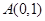 、
、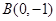 两点,以
两点,以 为直径的圆的方程为
为直径的圆的方程为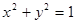 ,
,
由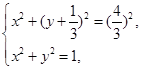 解得
解得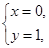
即两圆相切于点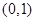 ,因此,所求的点
,因此,所求的点 如果存在,只能是
如果存在,只能是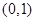 .8分
.8分
事实上,点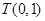 就是所求的点.
就是所求的点.
证明如下:
当 的斜率不存在时,以
的斜率不存在时,以 为直径的圆过点
为直径的圆过点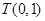 .9分
.9分
若 的斜率存在时,可设直线
的斜率存在时,可设直线 为
为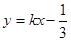 ,
,
由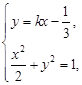 消去
消去 得
得 .
.
记点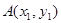 、
、 ,则
,则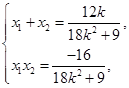 10分
10分
又因为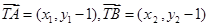 ,
,
所以
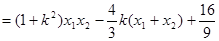
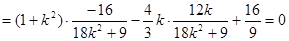 .
.
所以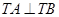 ,即以
,即以 为直径的圆恒过点
为直径的圆恒过点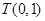 ,12分
,12分
所以在坐标平面上存在一个定点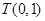 满足条件.13分
满足条件.13分
考点:直线与椭圆的位置关系
点评:主要是考查了解析几何中运用代数的方法来建立方程组结合韦达定理来研究位置关系的运用,属于中档题。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
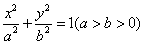 过点
过点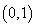 ,其长轴、焦距和短轴的长的平方依次成等差数列.直线
,其长轴、焦距和短轴的长的平方依次成等差数列.直线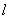 与
与 轴正半轴和
轴正半轴和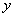 轴分别交于点
轴分别交于点 、
、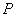 ,与椭圆分别交于点
,与椭圆分别交于点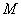 、
、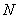 ,各点均不重合且满足
,各点均不重合且满足
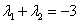 ,试证明:直线
,试证明:直线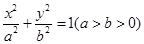 的离心率为
的离心率为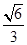 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为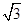 ,直线
,直线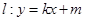 交椭圆于不同的两点
交椭圆于不同的两点 。
。 到直线
到直线 的距离为
的距离为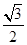 ,求
,求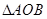 面积的最大值。
面积的最大值。
 ,m
,m 0),点P的轨迹加上M、N两点构成曲线C.
0),点P的轨迹加上M、N两点构成曲线C. ,曲线C过点Q (2,0) 斜率为
,曲线C过点Q (2,0) 斜率为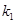 的直线
的直线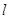 与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为
与曲线C交于不同的两点A﹑B,AB中点为R,直线OR (O为坐标原点)的斜率为 ,求证
,求证 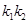 为定值;
为定值; ,且
,且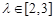 ,求
,求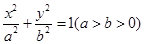 的左、右焦点分别为F1,F2,椭圆的离心率为
的左、右焦点分别为F1,F2,椭圆的离心率为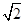 :2.(1)过点C(-1,0)且以向量
:2.(1)过点C(-1,0)且以向量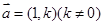 为方向向量的直线
为方向向量的直线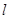 交椭圆于不同两点A、B,若
交椭圆于不同两点A、B,若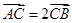 ,则当△OAB的面积最大时,求椭圆的方程。
,则当△OAB的面积最大时,求椭圆的方程。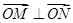 ,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.
,过原点O作直线MN的垂线OD,垂足为D,求点D的轨迹方程.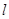 :
: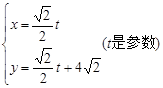 上的点向圆C:
上的点向圆C: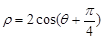 引切线,
引切线,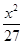 +
+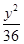 =1有公共的焦点,且与椭圆相交,它们的交点中一个交点的纵坐标是4,求双曲线的标准方程。
=1有公共的焦点,且与椭圆相交,它们的交点中一个交点的纵坐标是4,求双曲线的标准方程。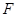 是椭圆
是椭圆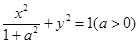 的右焦点,点
的右焦点,点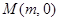 、
、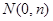 分别是
分别是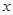 轴、
轴、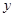 轴上的动点,且满足
轴上的动点,且满足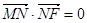 .若点
.若点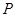 满足
满足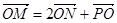 .
.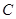 的方程;
的方程;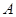 、
、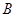 两点,直线
两点,直线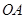 、
、 与直线
与直线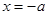 分别交
分别交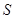 、
、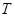 (
( 为坐标原点),试判断
为坐标原点),试判断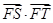 是否为定值?若是,求出这个定值;若不是,
是否为定值?若是,求出这个定值;若不是,