题目内容
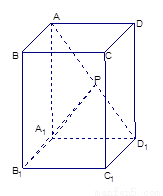
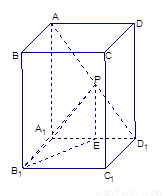
如图,已知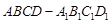 是底面为正方形的长方体,
是底面为正方形的长方体,
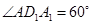 ,
, ,点
,点 是
是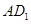 上的动点.
上的动点.
(1)试判断不论点 在
在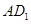 上的任何位置,是否都有平面[来源:学,科,网]
上的任何位置,是否都有平面[来源:学,科,网]
 垂直于平面
垂直于平面 ?并证明你的结论;
?并证明你的结论;
(2)当 为
为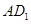 的中点时,求异面直线
的中点时,求异面直线 与
与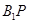 所成角的余弦值;
所成角的余弦值;
(3)求 与平面
与平面 所成角的正切值的最大值.
所成角的正切值的最大值.
【答案】
(1)不论点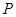 在
在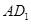 上的任何位置,都有平面
上的任何位置,都有平面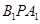 垂直于平面
垂直于平面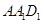 .
.
证明如下:由题意知,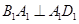 ,
,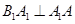 又
又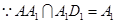
 平面
平面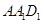 又
又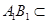 平面
平面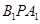
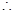 平面
平面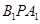
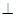 平面
平面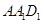 .
.
(2)解法一:过点P作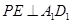 ,垂足为
,垂足为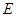 ,连结
,连结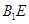 (如图),则
(如图),则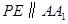 ,
,
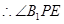 是异面直线
是异面直线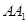 与
与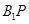 所成的角.
所成的角.
在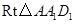 中 ∵
中 ∵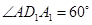 ∴
∴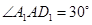
∴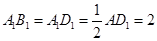 ,
, 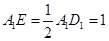 ,
,
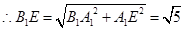 . 又
. 又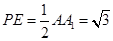 .
.
 在
在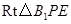 中,
中,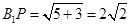
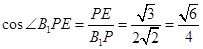 .
.
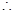 异面异面直线
异面异面直线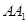 与
与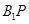 所成角的余弦值为
所成角的余弦值为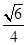 .
.
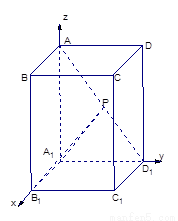 解法二:以
解法二:以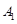 为原点,
为原点,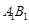 所在的直线为x轴建立空间直角坐标系如图示,则
所在的直线为x轴建立空间直角坐标系如图示,则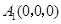 ,
,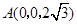 ,
,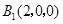 ,
,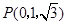 ,
,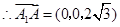 ,
,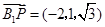
∴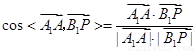
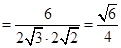 .
.
∴异面异面直线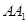 与
与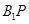 所成角的余弦值为
所成角的余弦值为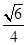 .
.
(3)由(1)知,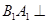 平面
平面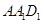 ,
,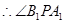 是
是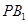 与平面
与平面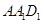 所成的角,
所成的角,
且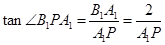 .
.
当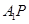 最小时,
最小时,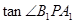 最大,这时
最大,这时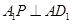 ,由
,由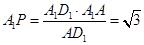
得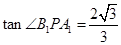 ,即
,即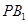 与平面
与平面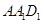 所成角的正切值的最大值
所成角的正切值的最大值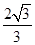 .
.
【解析】略

练习册系列答案
相关题目
 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为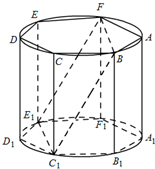 (2012•肇庆二模)如图,ABCDEF-A1B1C1D1E1F1是底面半径为1的圆柱的内接正六棱柱(底面是正六边形,侧棱垂直于底面),过FB作圆柱的截面交下底面于C1E1,已知
(2012•肇庆二模)如图,ABCDEF-A1B1C1D1E1F1是底面半径为1的圆柱的内接正六棱柱(底面是正六边形,侧棱垂直于底面),过FB作圆柱的截面交下底面于C1E1,已知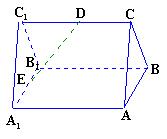
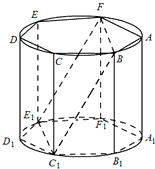 如图,ABCDEF-A1B1C1D1E1F1是底面半径为1的圆柱的内接正六棱柱(底面是正六边形,侧棱垂直于底面),过FB作圆柱的截面交下底面于C1E1,已知
如图,ABCDEF-A1B1C1D1E1F1是底面半径为1的圆柱的内接正六棱柱(底面是正六边形,侧棱垂直于底面),过FB作圆柱的截面交下底面于C1E1,已知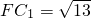 .
. .
.