题目内容
将3个小球任意地放入4个玻璃杯中,杯子中球的最多个数记为ξ,求ξ的分布列.?
解:依题意可知杯子中球的最多个数ξ的所有可能值为1,2,3.当ξ=1时,对应于4个杯子中恰有三个杯子各放一球的情形;当ξ=2时,对应于4个杯子中恰有一个杯子放两球的情形;当ξ=3时,对应于4个杯子恰有一个杯子放三个球的情形.?
当ξ=1时,P(ξ)=![]() ;?
;?
当ξ=2时,P(ξ)=![]() ;?
;?
当ξ=3时,P(ξ)=![]() .?
.?
可得ξ的分布列为?
ξ | 1 | 2 | 3 |
P |
|
|
|
点评:(1)解答本题关键在于得出杯子中球的最多个数ξ的所有可能值后,准确地计算出相应的概率,而在求概率时,常易出现失误,错误地认为P(ξ=1)=![]() ,P(ξ=2)=
,P(ξ=2)=
![]() ,P(ξ=3)=
,P(ξ=3)=![]() ;或P(ξ=1)=
;或P(ξ=1)=![]() ,P(ξ=2)=
,P(ξ=2)=![]() ,P(ξ=3)=
,P(ξ=3)=![]() ,等等.
,等等.
(2)由本题可以看出,求离散型随机变量的分布列,要求必须正确地求出相应的事件个数,即正确求出相应的排列组合数,所以,掌握好排列组合知识是学好分布列的基础与前提.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
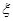 ,求
,求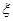 ,求
,求