题目内容
已知递增数列{an}满足an+1•an-1=an2(n≥2,n∈N),其前10项和等于50,前15项的和为210,则其前5项的和为( )
分析:根据题意,由an+1•an-1=an2,易得{an}为等比数列;进而根据等比数列前n项和的性质可得S5、S10-S5、S15-S10也是等比数列;即有(50-S5)2=S5×(210-50),解可得S5=10或250,又由{an}是递增数列,则S5<S10,对求出的S5取舍即可得答案.
解答:解:根据题意,由an+1•an-1=an2,且{an}是递增数列,
可得{an}为等比数列;
则S5、S10-S5、S15-S10,也是等比数列;
即S5、50-S5、210-50,三项等比数列,即有(50-S5)2=S5×(210-50),
解可得S5=10或250,
又由{an}是递增数列,
∴S5=10,
故选A.
可得{an}为等比数列;
则S5、S10-S5、S15-S10,也是等比数列;
即S5、50-S5、210-50,三项等比数列,即有(50-S5)2=S5×(210-50),
解可得S5=10或250,
又由{an}是递增数列,
∴S5=10,
故选A.
点评:本题考查等比关系的确定以及等比数列前n项和的性质,注意牢记并灵活运用等比数列的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
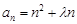 ,则实数λ的取值范围是( )
,则实数λ的取值范围是( )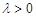 B.
B.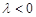 C.
C.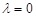 D.
D.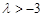
 …
…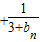 ,证明:
,证明: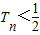 .
.