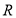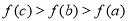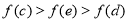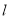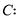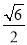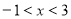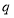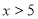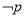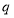题目内容
某社团组织20名志愿者利用周末和节假日参加社会公益活动，志愿者中，年龄在20至40岁的有12人，年龄大于40岁的有8人.
（1）在志愿者中用分层抽样方法随机抽取5名，年龄大于40岁的应该抽取几名?
（2）上述抽取的5名志愿者中任取2名，求取出的2人中恰有1人年龄大于40岁的概率.
（1）2人；（2）恰有1人年龄大于40岁的概率为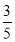
.
【解析】
试题分析：（1）利用分层抽样中总体抽样比与各层中的抽样比相等这一特点，先求出抽样比例，然后用年龄大于40岁的人数乘以抽样比即可得到在年龄大于40岁的志愿者中抽取的人数；（2）这是古典概型的概率问题，先用列举法确定从5名志愿者中任取2名的所有可能有多少种，然后确定这2人中恰有1人年龄大于40岁的情况又有多少种，最后按照古典概型的概率计算公式计算即可.
试题解析：(1)若在志愿者中随机抽取5名，则抽取比例为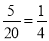
2分
∴年龄大于40岁的应该抽取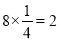
人 4分
(2)上述抽取的5名志愿者中，年龄在20至40岁的有3人，记为1，2，3
年龄大于40岁的有2人，记为4，5 6分
从中任取2名，所有可能的基本事件为：
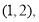
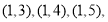
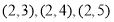
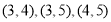共10种 8分
其中恰有1人年龄大于40岁的事件有
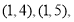
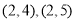
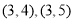共6种 10分
∴恰有1人年龄大于40岁的概率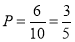
12分.
考点：1.随机抽样；2.古典概率.
练习册系列答案
阅读快车系列答案
相关题目
