题目内容
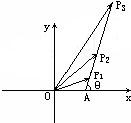 如图所示,在复平面内有三点P1,P2,P3对应的复数分别为1+a,1+2a,1+3a,且|a|=2,O为原点,求当S△P1OP2+S△P2OP3=2时,对应的复数a.
如图所示,在复平面内有三点P1,P2,P3对应的复数分别为1+a,1+2a,1+3a,且|a|=2,O为原点,求当S△P1OP2+S△P2OP3=2时,对应的复数a.
分析:如图,A点对应的复数为1,可知有向线段AP1,AP2,AP3对应的复数为a,2a,3a,因此A,P1,P2,P3共线,利用面积关系:
S△P1OP2+S△P2OP3=S△OAP3-S△OAP1,可得到关系式,再来求解就可以了.
S△P1OP2+S△P2OP3=S△OAP3-S△OAP1,可得到关系式,再来求解就可以了.
解答:解:AP1,AP2,AP3对应的复数为a,2a,3a,且它们有相同的辐角主值θ,即A,P1,P2,P3共线.
∴S△AOP3=
|
|•|
|sin•θ
=
•1•|3a|=sinθ=3sinθ
S△OAP1=
|
|•|
|
=
•1•|a|•sinθ=sinθ
显然S△P1OP2+S△P2OP3=S△OAP3-S△OAP1=2sinθ
从而2sinθ=2
sinθ=1,即θ=
[∵θ∈(0,2π)]
因此有a=±2i.
∴S△AOP3=
| 1 |
| 2 |
| OA |
| AP3 |
=
| 1 |
| 2 |
S△OAP1=
| 1 |
| 2 |
| OA |
| AP1 |
=
| 1 |
| 2 |
显然S△P1OP2+S△P2OP3=S△OAP3-S△OAP1=2sinθ
从而2sinθ=2
sinθ=1,即θ=
| π |
| 2 |
因此有a=±2i.
点评:本题考查复数的概念以及运算,复数模的求法,复数的辐角的概念,三角形的面积的综合问题,

练习册系列答案
相关题目
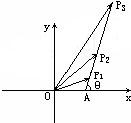 如图所示,在复平面内有三点P1,P2,P3对应的复数分别为1+a,1+2a,1+3a,且|a|=2,O为原点,求当
如图所示,在复平面内有三点P1,P2,P3对应的复数分别为1+a,1+2a,1+3a,且|a|=2,O为原点,求当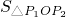 +
+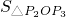 =2时,对应的复数a.
=2时,对应的复数a. +
+ =2时,对应的复数a.
=2时,对应的复数a.