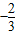Question

直线l与两直线y=1，x-y-7=0分别交于A，B两点，若直线AB的中点是M（1，-1），则直线l的斜率为

 

．

Answer 1

分析：设出直线l的斜率为k，又直线l过M点，写出直线l的方程，然后分别联立直线l与已知的两方程，分别表示出A和B的坐标，根据中点坐标公式表示出M的横坐标，让表示的横坐标等于1列出关于k的方程，求出方程的解即可得到k的值即为直线的斜率．

解答：解：设直线l的斜率为k，又直线l过M（1，-1），则直线l的方程为y+1=k（x-1），
联立直线l与y=1，得到

y+1=kx-k y=1

，
解得x=

2+k

k

，
∴A（

2+k

k

，1）；
联立直线l与x-y-7=0，得到

x-y-7=0 y+1=kx-k

，
解得x=

6-k

1-k

，y=

6k-1

1-k

，
∴B（

6-k

1-k

，

6k-1

1-k

），
又线段AB的中点M（1，-1），
∴

6-k 1-k + 2+k k 2 =1 1+ 6k-1 1-k 2 =-1

，解得k=-

2

3

．
故答案为：-

2

3

点评：本题主要考查直线斜率的求法，根据两直线方程求两直线的交点坐标，灵活运用中点坐标公式化简求值是解决本题的关键．