题目内容
广东某品牌玩具企业的产品以往专销欧州市场,在欧债危机的影响下,欧州市场的销量受到严重影响,该企业在政府的大力扶助下积极开拓国内市场,主动投入内销产品的研制开发,并基本形成了市场规模,自2010年9月以来的第n个月(2010年9月为每一个月),产品的内销量、出口量和销售总量(内销量与出口量的和)分别为bn、cn和an(单位万件),分析销售统计数据发现形成如下营销趋势:bn+1=aan,cn+1=an+b
(其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.
(1)求a,b的值,并写出an+1与an满足的关系式;
(2)如果该企业产品的销售总量an呈现递增趋势,且控制在2万件以内,企业的运作正常且不会出现资金危机;试证明:an<an+1<2.
(3)试求从2010年9月份以来的第n个月的销售总量an关于n的表达式.
| a | 2 n |
(1)求a,b的值,并写出an+1与an满足的关系式;
(2)如果该企业产品的销售总量an呈现递增趋势,且控制在2万件以内,企业的运作正常且不会出现资金危机;试证明:an<an+1<2.
(3)试求从2010年9月份以来的第n个月的销售总量an关于n的表达式.
分析:(1)依题意:an+1=bn+1+cn+1=aan+an+ban2,推出a+1+b=
,以及
a+
+b(
)2=
,求出a=1,b=-
得到an+1=2an-
an2(n∈N*).
(2)证法(Ⅰ)利用an+1=2an-
an2=-
(an-2)2+2≤2.可推得a1=2与a1=1矛盾.故an+1<2,于是an<2,通过单调性证明an<an+1<2.
方法(Ⅱ)用数学归纳法证明(ⅰ)验证n=1时a1<a2<2成立,(ⅱ)假设n=k时,ak<ak+1<2成立.证明n=k+1时不等式也成立.
(3)通过an+1=2an-
an2,推出{lg(2-an+1)-lg2}为等比数列,公比为2,然后求出an=2-(
)2n-1-1(n∈N*).
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)证法(Ⅰ)利用an+1=2an-
| 1 |
| 2 |
| 1 |
| 2 |
方法(Ⅱ)用数学归纳法证明(ⅰ)验证n=1时a1<a2<2成立,(ⅱ)假设n=k时,ak<ak+1<2成立.证明n=k+1时不等式也成立.
(3)通过an+1=2an-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)依题意:an+1=bn+1+cn+1=aan+an+ban2,
又a2=aa1+a1+ba12,∴a+1+b=
…①
又a3=aa2+a2+ba22,∴
a+
+b(
)2=
…②
解①②得a=1,b=-
从而an+1=2an-
an2(n∈N*)…(4分)
(2)证法(Ⅰ)由于an+1=2an-
an2=-
(an-2)2+2≤2.
但an+1≠2,否则可推得a1=2与a1=1矛盾.故an+1<2,于是an<2,
又an+1-an=-
an2+2an-an=-
an(an-2)>0,
所以an+1>an,从而an<an+1<2.…(9分)
方法(Ⅱ)用数学归纳法
(ⅰ)当n=1时,a1=1,a2=1.5,显然a1<a2<2成立,
(ⅱ)假设n=k时,ak<ak+1<2成立.
由于函数f(x)=-
x2+2x=-
(x-2)2+2在[0,2]上为增函数,
则f(ak)<f(ak+1)<f(2)即
ak(4-ak)<
ak+1(4-ak+1)<
×2×(4-2)
即ak+1<ak+2<2成立.综上可得n∈N*有an<an+1<2.…(9分)
(3)由an+1=2an-
an2得2(an+1-2)=-(an-2)2,即(2-an+1)=
(2-an)2,
又由(2)知an<an+1<2,可知2-an+1>0,2-an>0,
则lg(2-an+1)=2lg(2-an)-lg2,∴lg(2-an+1)-lg2=2[lg(2-an)-lg2]
即{lg(2-an+1)-lg2}为等比数列,公比为2,首项为lg(2-a1)-lg2=-lg2
故lg(2-an)-lg2=(-lg2)•2n-1,∴an=2-(
)2n-1-1(n∈N*)为所求.…(13分)
又a2=aa1+a1+ba12,∴a+1+b=
| 3 |
| 2 |
又a3=aa2+a2+ba22,∴
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 8 |
解①②得a=1,b=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)证法(Ⅰ)由于an+1=2an-
| 1 |
| 2 |
| 1 |
| 2 |
但an+1≠2,否则可推得a1=2与a1=1矛盾.故an+1<2,于是an<2,
又an+1-an=-
| 1 |
| 2 |
| 1 |
| 2 |
所以an+1>an,从而an<an+1<2.…(9分)
方法(Ⅱ)用数学归纳法
(ⅰ)当n=1时,a1=1,a2=1.5,显然a1<a2<2成立,
(ⅱ)假设n=k时,ak<ak+1<2成立.
由于函数f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
则f(ak)<f(ak+1)<f(2)即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即ak+1<ak+2<2成立.综上可得n∈N*有an<an+1<2.…(9分)
(3)由an+1=2an-
| 1 |
| 2 |
| 1 |
| 2 |
又由(2)知an<an+1<2,可知2-an+1>0,2-an>0,
则lg(2-an+1)=2lg(2-an)-lg2,∴lg(2-an+1)-lg2=2[lg(2-an)-lg2]
即{lg(2-an+1)-lg2}为等比数列,公比为2,首项为lg(2-a1)-lg2=-lg2
故lg(2-an)-lg2=(-lg2)•2n-1,∴an=2-(
| 1 |
| 2 |
点评:本题考查数列的关系式,数学归纳法的应用,数列的函数特征,函数的单调性的应用,数列通项公式的求法,考查转化思想,逻辑推理能力.

练习册系列答案
相关题目
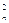 (其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.
(其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.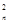 (其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.
(其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.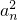 (其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.
(其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件. (其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.
(其中a、b为常数),且a1=1万件,a2=1.5万件,a3=1.875万件.