题目内容
 某超市在一段时间内的某种商品的价格x(元)与销售量y(kg)之间的一组数据如下表所示:
某超市在一段时间内的某种商品的价格x(元)与销售量y(kg)之间的一组数据如下表所示:| 价格x(元) | 11.4 | 11.6 | 11.8 | 12.0 | 12.2 |
| 销售量y(kg) | 112 | 110 | 107 | 105 | 103 |
(Ⅱ)求出y对x的回归的直线方程;
(Ⅲ)当价格定为11.9元时,预测销售量大约是多少?
| ||||||||||||||||||||||||||||||||
分析:(I)根据表中给的数据,在直角坐标系中画出散点图;
(II)将表中所给的数据处理后代入公式,求出
,
的值,进一步求出y对x的回归直线方程.
(III))将x=11.9代入求出的y对x的回归的直线方程得y,即得到价格定为11.9万元,预测需求量.
(II)将表中所给的数据处理后代入公式,求出
 |
| b |
 |
| a |
(III))将x=11.9代入求出的y对x的回归的直线方程得y,即得到价格定为11.9万元,预测需求量.
解答: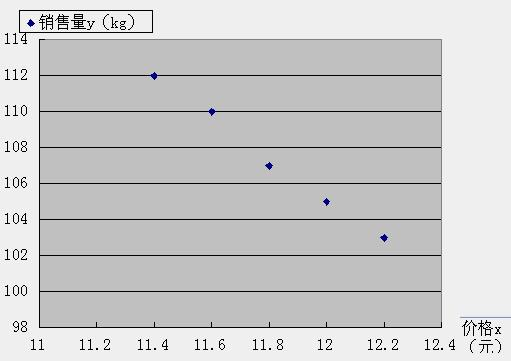 解:(I)根据表中给的数据,在直角坐标系中画出散点图.(II)对原数据处理如下:
解:(I)根据表中给的数据,在直角坐标系中画出散点图.(II)对原数据处理如下:
'=0,
=0.4,∴
=-11.5,∴
=
-
=0.4-(-11.5)×0=0.4,
∴y'对x'的回归的直线方程y'=-11.5x'+0.4,
∴y对x的回归的直线方程y-107=-11.5(x-11.8)+0.4,
即y=-11.5x+243.1.
(III)当x=11.9时,y=106.25,
∴当价格定为11.9元时,预测销售量大约是106.25kg.
 解:(I)根据表中给的数据,在直角坐标系中画出散点图.(II)对原数据处理如下:
解:(I)根据表中给的数据,在直角坐标系中画出散点图.(II)对原数据处理如下:| x-11.8(元) | -0.4 | -0.2 | 0 | 0.2 | 0.4 |
| y-107(kg) | 5 | 3 | 0 | -2 | -4 |
. |
| x |
. |
| y′ |
 |
| b |
 |
| a |
. |
| y′ |
 |
| b |
. |
| x′ |
∴y'对x'的回归的直线方程y'=-11.5x'+0.4,
∴y对x的回归的直线方程y-107=-11.5(x-11.8)+0.4,
即y=-11.5x+243.1.
(III)当x=11.9时,y=106.25,
∴当价格定为11.9元时,预测销售量大约是106.25kg.
点评:本题考查线性回归方程,是一个基础题,解题的关键是利用最小二乘法写出线性回归系数,注意解题的运算过程不要出错.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目

 某超市在一段时间内的某种商品的价格x(元)与销售量y(kg)之间的一组数据如下表所示:
某超市在一段时间内的某种商品的价格x(元)与销售量y(kg)之间的一组数据如下表所示: