题目内容

若偶函数f（x）在（-∞，0]内单调递减，则不等式f（-1）＜f（lgx）的解集是（　　）
A、（0，10）
B、(
1
10
，10)
C、(
1
10
，+∞)
D、（0，
1
10
）∪（10，+∞）
分析：偶函数f（x）在（-∞，0]内单调递减，根据偶函数的对称性知，它在（0，-∞内单调递增，据此画出函数的图象，结合函数的奇偶性、单调性解决．
解答：根据题意画图：
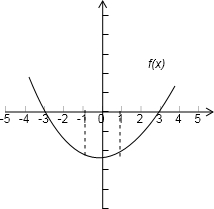
精英家教网
由图得，lgx＞1或lgx＜-1
∴x∈（0，
1
10
）∪（10，+∞）
故选D．
点评：函数的奇偶性单调性在函数的图象上有着非常直观的形象，数与形结合帮助我们快速解决问题．
练习册系列答案
相关题目
若偶函数f（x）在区间[-1，0]上是减函数，α、β是锐角三角形的两个内角，且α≠β，则下列不等式中正确的是（　　）
A、f（cosα）＞f（cosβ）B、f（sinα）＞f（cosβ）C、f（sinα）＞f（sinβ）D、f（cosα）＞f（sinβ）
若偶函数f（x）在（0，+∞）上是增函数，则a=f(-
2
)，b=f(
π
2
)，c=f(
3
2
)的大小关系是（　　）
A、b＜a＜c
B、b＜c＜a
C、a＜c＜b
D、c＜a＜b
若偶函数f（x）在（-∞，0）上是减函数，则下列关系式中成立的是（　　）
若偶函数f（x）在（-∞，-1]上是增函数，则下列关系式中成立的是（　　）
若偶函数f（x）在[0，2]上单调递增则（　　）
A、f(-1)＞f(log0.5
1
4
)＞f(lg0.5)
B、f(lg0.5)＞f(-1)＞f(log0.5
1
4
)
C、f(log0.5
1
4
)＞f(-1)＞f(lg0.5)
D、f(lg0.5)＞f(log0.5
1
4
)＞f(-1)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网