题目内容
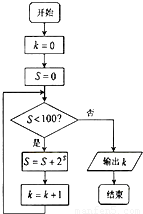
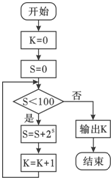 如图,已知K为如图所示的程序框图输出结果,二项式(xk+
如图,已知K为如图所示的程序框图输出结果,二项式(xk+| 1 | x |
分析:先利用程序框图输出的结果得出k的值,再利用二项展开式的通项公式求出展开式的通项,令x的指数为0方程有解.由于n,r都是整数求出最小的正整数n.
解答:解:分析程序中各变量、各语句的作用,
再根据流程图所示的顺序,可知:第一次运行后S=0+20=1,K=1;
第二次运行后S=1+21=3,K=2;
第三次运行后S=3+23=11,K=3;
第四次运行后S=11+211>100,K=4,
∴K=4
展开式的通项为Tr+1=Cnrx4n-5r
令4n-5r=0据题意此方程有解,∴n=
,
当r=4时,n最小为5.
故选B.
再根据流程图所示的顺序,可知:第一次运行后S=0+20=1,K=1;
第二次运行后S=1+21=3,K=2;
第三次运行后S=3+23=11,K=3;
第四次运行后S=11+211>100,K=4,
∴K=4
展开式的通项为Tr+1=Cnrx4n-5r
令4n-5r=0据题意此方程有解,∴n=
| 5r |
| 4 |
当r=4时,n最小为5.
故选B.
点评:本题考查了循环结构,二项展开式的通项公式,解题的关键是根据程序框图求出K值.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
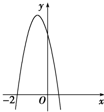 已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f′(x)的图象经过点(-2,0),如图所示.
已知函数f(x)=ax3+bx2+4x的极小值为-8,其导函数y=f′(x)的图象经过点(-2,0),如图所示. 已知K为如图所示的程序框图输出的结果,二项式(xk
已知K为如图所示的程序框图输出的结果,二项式(xk

 )n的展开式中含有非零常数项,则正整数n的最小值为 .
)n的展开式中含有非零常数项,则正整数n的最小值为 .