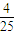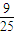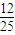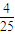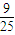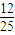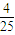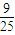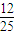题目内容
分别把写有1,2,3,4数字的四张纸片放入一盒中,每次取一张记数字为m,放回后再取一张记数字为n,设P(m,n)为平面中的点,则点P(m,n)∈{(x,y)|9x2+16y2≤144}的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:本题是一个等可能事件的概率,试验发生包含的事件数有4×4种结果,满足条件的事件是P(m,n)∈{(x,y)|9x2+16y2≤144}列举出满足条件的所有的事件共有4种结果,根据等可能事件的概率公式得到结果.
解答:解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件数有4×4=16种结果,
满足条件的事件是P(m,n)∈{(x,y)|9x2+16y2≤144}
列举出满足条件的所有的事件(1,1)(1,2)(2,1)(2,2)共有4种结果,
∴满足条件的概率是
=
,
故选D
试验发生包含的事件数有4×4=16种结果,
满足条件的事件是P(m,n)∈{(x,y)|9x2+16y2≤144}
列举出满足条件的所有的事件(1,1)(1,2)(2,1)(2,2)共有4种结果,
∴满足条件的概率是
| 4 |
| 16 |
| 1 |
| 4 |
故选D
点评:本题考查等可能事件的概率,考查椭圆的性质,是一个以概率为载体,而考查圆锥曲线的问题,是一个综合题目.

练习册系列答案
相关题目