题目内容
已知A1,A2是椭圆
+
=1(a>b>0)长轴的两个端点,B是它短轴的一个端点,如果
与
的夹角不小于
,则该椭圆的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| BA1 |
| BA2 |
| 2π |
| 3 |
分析:先将已知条件
与
的夹角不小于
转化为∠A1BO≥
,为建立a、b、c间的不等式创造条件,再在Rt△BOA1中,将∠A1BO≥
转化为
≥
,最后利用椭圆中b2=a2-c2将不等式转化为离心率不等式,解不等式得离心率取值范围
| BA1 |
| BA2 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| a |
| b |
| 3 |
解答:解:设椭圆中心为O,∵
与
的夹角不小于
,即∠A1BO≥
在Rt△BOA1中,|OA1|=a,|OB|=b,tan∠A1BO=
=
≥tan(
)=
即a≥
b,即a2≥3b2,即a2≥3(a2-c2)
∴2a2≤3c2∴e2≥
∴e≥
,又∵椭圆的离心率0<e<1
∴该椭圆的离心率的取值范围是[
,1)
故选C.
| BA1 |
| BA2 |
| 2π |
| 3 |
| π |
| 3 |
在Rt△BOA1中,|OA1|=a,|OB|=b,tan∠A1BO=
| |OA 1| |
| |OB| |
| a |
| b |
| π |
| 3 |
| 3 |
即a≥
| 3 |
∴2a2≤3c2∴e2≥
| 2 |
| 3 |
∴e≥
| ||
| 3 |
∴该椭圆的离心率的取值范围是[
| ||
| 3 |
故选C.
点评:本题考察了椭圆的标准方程和椭圆的几何性质,特别是求椭圆离心率的方法,解题时要认真总结规律,提高解题速度

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 长轴的两个端点,B是它短轴的一个端点,如果
长轴的两个端点,B是它短轴的一个端点,如果 与
与 的夹角不小于
的夹角不小于 ,则该椭圆的离心率的取值范围是( )
,则该椭圆的离心率的取值范围是( )



 长轴的两个端点,B是它短轴的一个端点,如果
长轴的两个端点,B是它短轴的一个端点,如果 与
与 的夹角不小于
的夹角不小于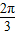 ,则该椭圆的离心率的取值范围是( )
,则该椭圆的离心率的取值范围是( )



 长轴的两个端点,B是它短轴的一个端点,如果
长轴的两个端点,B是它短轴的一个端点,如果 与
与 的夹角不小于
的夹角不小于 ,则该椭圆的离心率的取值范围是( )
,则该椭圆的离心率的取值范围是( )



 长轴的两个端点,B是它短轴的一个端点,如果
长轴的两个端点,B是它短轴的一个端点,如果 与
与 的夹角不小于
的夹角不小于 ,则该椭圆的离心率的取值范围是( )
,则该椭圆的离心率的取值范围是( )


